点、线、多边形之间的位置关系
点与多边形的位置关系:
光线投射方法(Ray casting algorithm);从这个点引出一根“射线”,与多边形的任意若干条边相交,累计相交的边的数目,如果是奇数,那么点就在多边形内,否则点就在多边形外。如下图所示:
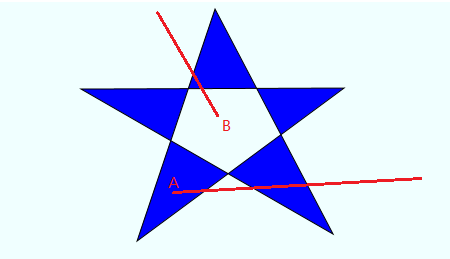
Point-In-Polygon Algorithm — Determining Whether A Point Is Inside A Complex Polygon这篇文章解释了光线投射方法,并且提出下面两种情况应该如何解决:
- 射线正好穿过多边形顶点:如果顶点正好通过射线,就认为该点在射线的上方,从而保证该点只被计算一次。
- 射线正好跟一条边重合:道理与上面相同。如果一条边正好在射线上,就认为该边在射线的上方,从而保证这个地方也只计算一次。
Stack Overflow上面有算法实现: How can I determine whether a 2D Point is within a Polygon?
边界具有方向性的多边形
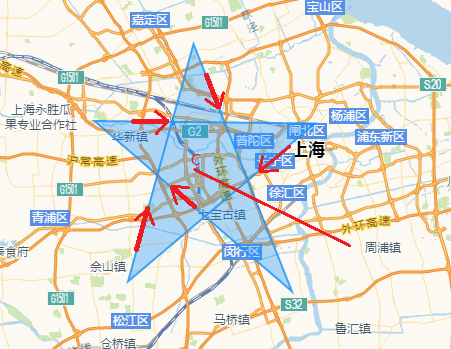
除了光线投射方法(Ray casting algorithm),还有Winding number algorithm(nonzero-rule algorithm)。这个方法用于边界有方向的多边形的判断。
从待检测点引出一根“射线”,与多边形的任意若干条边相交,计数初始化为0,若相交处被多边形的边从左到右切过,计数+1,若相交处被多边形的边从右到左切过,计数-1,最后检查计数,如果是0,点在多边形外,如果非0,点在多边形内。
线段与多边形的位置关系:
有算法,有代码,而且思路清晰。
思路:解决了下面三个问题:
- 问题一:点与线段的关系
- 问题二:线段与线段的关系
- 问题三:点与多边形的关系
就自然可以解决线段与多边形的位置关系了。
更一般化的方法:
给你n个多边形,这些多边形包括线段,三角形,矩形,正方形,和其他多边形. 然后要你输出他们之间相交的情况. 且多边形自己的边不会相交,且三角形不会退化成线段.
判断两个图形是否相交,只需要判断他们中的任意两条边是否有交点即可(线段相交判定).
如果两个多边形都为凸多边形,则有更简单的方法:
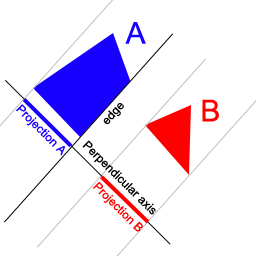
For each edge of both polygons:
- Find the axis perpendicular to the current edge.
- Project both polygons on that axis.
- If these projections don’t overlap, the polygons don’t intersect (exit the loop).