程序员的数学基础课（黄申）

01-开篇词 (1讲)

00丨开篇词丨作为程序员，为什么你应该学好数学？

02-导读 (1讲)

00丨导读：程序员应该怎么学数学？

03-基础思想篇 (18讲)

01丨二进制：不了解计算机的源头，你学什么编程

02丨余数：原来取余操作本身就是个哈希函数

03丨迭代法：不用编程语言的自带函数，你会如何计算平方根？

迭代法有什么具体应用？

迭代法在无论是在数学，还是计算机领域都有很广泛的应用。大体上，迭代法可以运用在以下几个方面：

  1. 求数值的精确或者近似解。典型的方法包括二分法（Bisection method）和牛顿迭代法（Newton’s method）。
  2. 在一定范围内查找目标值。典型的方法包括二分查找。
  3. 机器学习算法中的迭代。相关的算法或者模型有很多，比如 K- 均值算法（K-means clustering）、PageRank 的马尔科夫链（Markov chain）、梯度下降法（Gradient descent）等等。迭代法之所以在机器学习中有广泛的应用，是因为很多时候机器学习的过程，就是根据已知的数据和一定的假设，求一个局部最优解。而迭代法可以帮助学习算法逐步搜索，直至发现这种解。

04丨数学归纳法：如何用数学归纳提升代码的运行效率？

数学归纳法的一般步骤是这样的：

  1. 证明基本情况（通常是n=1的时候）是否成立；
  2. 假设n=k−1成立，再证明n=k也是成立的（k为任意大于1的自然数）。

和使用迭代法的计算相比，数学归纳法最大的特点就在于“归纳”二字。它已经总结出了规律。只要我们能够证明这个规律是正确的，就没有必要进行逐步的推算，可以节省很多时间和资源。

递归调用的代码和数学归纳法的逻辑是一致的。

递归和数学归纳法的核心思想

复杂的问题，每次都解决一点点，并将剩下的任务转化成为更简单的问题等待下次求解，如此反复，直到最简单的形式。

05丨递归（上）：泛化数学归纳，如何将复杂问题简单化？

06丨递归（下）：分而治之，从归并排序到MapReduce

对于一些复杂问题，我们可以先分析一下，它们是否可以简化为某些更小的、更简单的子问题来解决，这是一般思路。如果可以，那就意味着我们仍然可以使用递归的核心思想，将复杂的问题逐步简化成最基本的情况来求解。

因此，今天我会从归并排序开始，延伸到多台机器的并行处理，详细讲讲递归思想在“分而治之”这个领域的应用。

归并排序

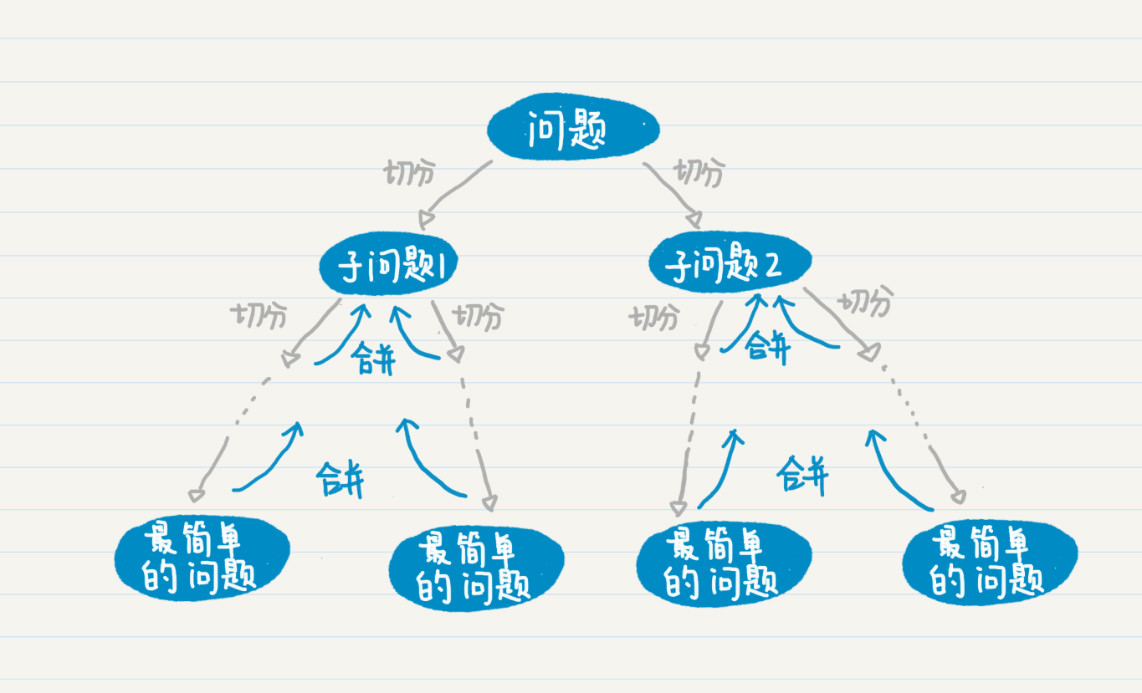
20220531归并排序模型.jpeg

我们可以在归并排序中引入了分而治之（Divide and Conquer）的思想。分而治之，我们通常简称为分治。它的思想就是，将一个复杂的问题，分解成两个甚至多个规模相同或类似的子问题，然后对这些子问题再进一步细分，直到最后的子问题变得很简单，很容易就能被求解出来，这样这个复杂的问题就求解出来了。

分布式系统中的分治思想

分而治之更有趣的应用其实是在分布式系统中。

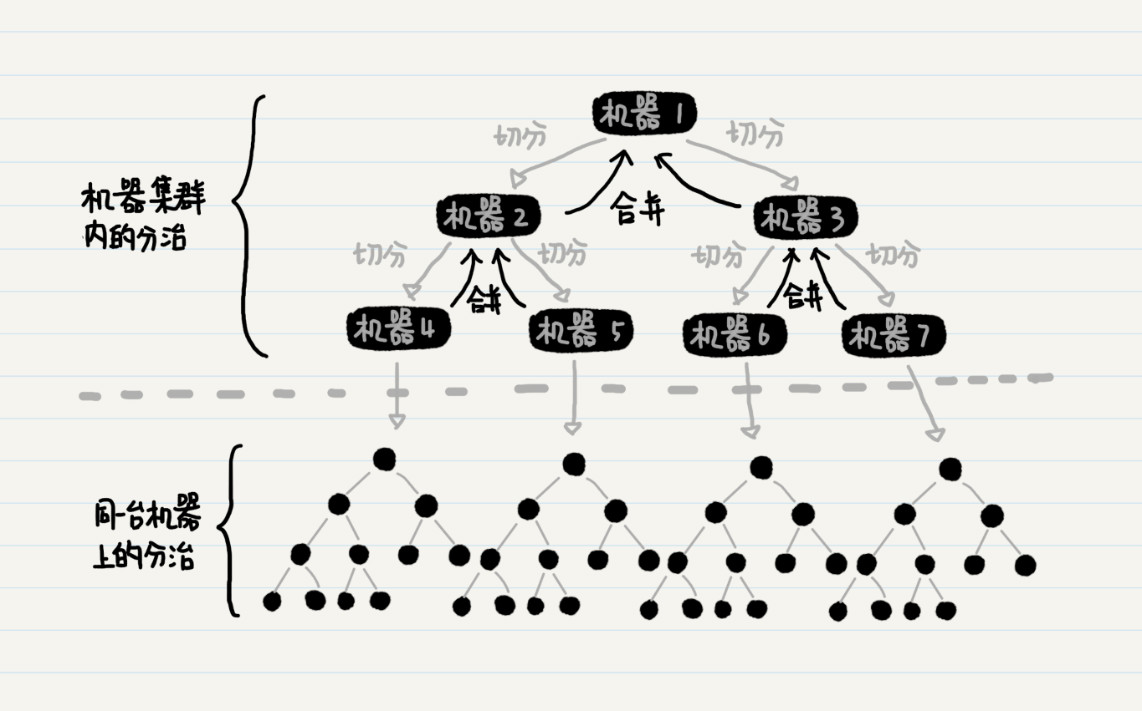
例如，当需要排序的数组很大（比如达到 1024GB 的时候），我们没法把这些数据都塞入一台普通机器的内存里。该怎么办呢？有一个办法，我们可以把这个超级大的数据集，分解为多个更小的数据集（比如 16GB 或者更小），然后分配到多台机器，让它们并行地处理。

等所有机器处理完后，中央服务器再进行结果的合并。由于多个小任务间不会相互干扰，可以同时处理，这样会大大增加处理的速度，减少等待时间。

在单台机器上实现归并排序的时候，我们只需要在递归函数内，实现数据分组以及合并就行了。而在多个机器之间分配数据的时候，递归函数内除了分组及合并，还要负责把数据分发到某台机器上。

20220531分而治之分布式系统.jpeg

07丨排列：如何让计算机学会“田忌赛马”？

08丨组合：如何让计算机安排世界杯的赛程？

09丨动态规划（上）：如何实现基于编辑距离的查询推荐？

聊聊查询推荐（Query Suggestion）的实现过程，以及它所使用的数学思想，动态规划（Dynamic Programming）。

编辑距离

搜索下拉提示和关键词纠错，这两个功能其实就是查询推荐。查询推荐的核心思想其实就是，对于用户的输入，查找相似的关键词并进行返回。而测量拉丁文的文本相似度，最常用的指标是编辑距离（Edit Distance）。

编辑距离是指由一个字符串转成另一个字符串所需的最少编辑操作次数。

状态转移

我用mouuse和mouse的例子。我把mouuse的字符数组作为表格的行，每一行表示其中一个字母，而mouse的字符数组作为列，每列表示其中一个字母，这样就得到下面这个表格。

20220531编辑距离状态转移.png

10丨动态规划（下）：如何求得状态转移方程并进行编程实现？

状态转移方程

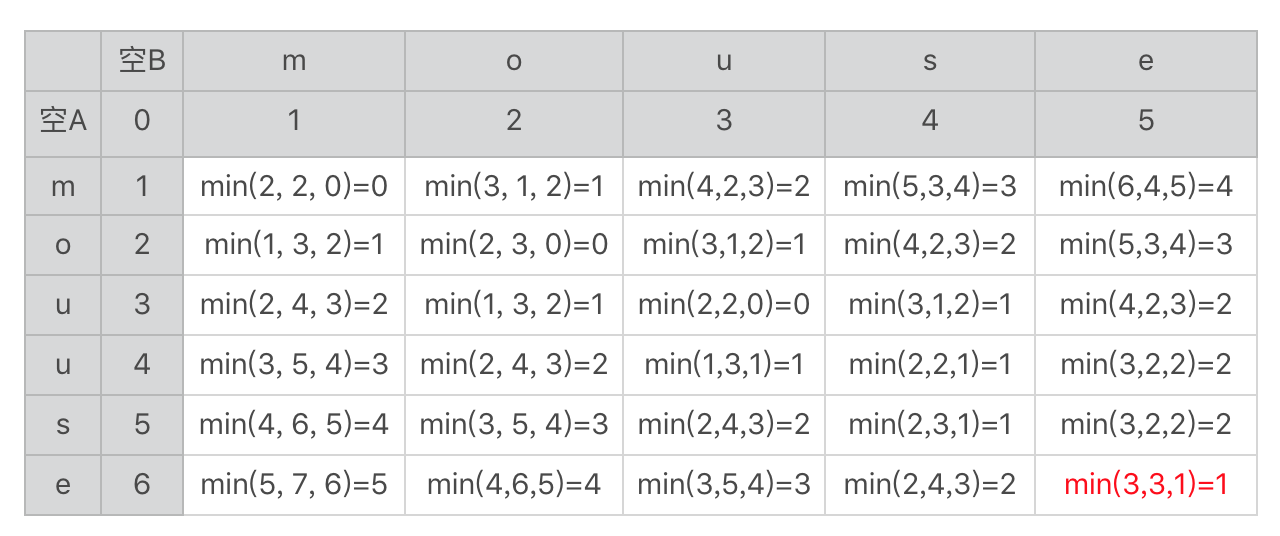
20220531编辑距离状态转移方程.png

这里面求最小值的min函数里有三个参数，分别对应我们上节讲的三种情况的编辑距离，分别是：替换、插入和删除字符。在表格的右下角我标出了两个字符串的编辑距离1。

我们假设字符数组A[]和B[]分别表示字符串A和B，A[i]表示字符串A中第i个位置的字符，B[i]表示字符串B中第i个位置的字符。二维数组d[,]表示刚刚用于推导的二维表格，而d[i,j]表示这张表格中第i行、第j列求得的最终编辑距离。函数r(i, j)表示替换时产生的编辑距离。如果A[i]和B[j]相同，函数的返回值为0，否则返回值为1。

有了这些定义，下面我们用迭代来表达上述的推导过程。

  1. 如果i为0，且j也为0，那么d[i, j]为0。
  2. 如果i为0，且j大于0，那么d[i, j]为j。
  3. 如果i大于0，且j为0，那么d[i, j]为i。
  4. 如果i大于0，且j大于0，那么d[i, j]=min(d[i-1, j] + 1, d[i, j-1] + 1, d[i-1, j-1] + r(i, j))。

这里面最关键的一步是d[i, j]=min(d[i-1, j] + 1, d[i, j-1] + 1, d[i-1, j-1] + r(i, j))。这个表达式表示的是动态规划中从上一个状态到下一个状态之间可能存在的一些变化，以及基于这些变化的最终决策结果。我们把这样的表达式称为状态转移方程。

总结

通过这两节的内容，我讲述了动态规划主要的思想和应用。如果仅仅看这两个案例，也许你觉得动态规划不难理解。不过，在实际应用中，你可能会产生这些疑问：什么时候该用动态规划？这个问题可以用动态规划解决啊，为什么我没想到？我这里就讲一些我个人的经验。

首先，如果一个问题有很多种可能，看上去需要使用排列或组合的思想，但是最终求的只是某种最优解（例如最小值、最大值、最短子串、最长子串等等），那么你不妨试试是否可以使用动态规划。

其次，状态转移方程是个关键。你可以用状态转移表来帮助自己理解整个过程。如果能找到准确的转移方程，那么离最终的代码实现就不远了。

11丨树的深度优先搜索（上）：如何才能高效率地查字典？

12丨树的深度优先搜索（下）：如何才能高效率地查字典？

13丨树的广度优先搜索（上）：人际关系的六度理论是真的吗？

14丨树的广度优先搜索（下）：为什么双向广度优先搜索的效率更高？

如何更高效地求两个用户间的最短路径？

基本的做法是，从其中一个人出发，进行广度优先搜索，看看另一个人是否在其中。如果不幸的话，两个人相距六度，那么即使是广度优先搜索，同样要达到万亿级的数量。

那究竟该如何更高效地求得两个用户的最短路径呢？我们先看看，影响效率的问题在哪里？很显然，随着社会关系的度数增加，好友数量是呈指数级增长的。所以，如果我们可以控制这种指数级的增长，那么就可以控制潜在好友的数量，达到提升效率的目的。

如何控制这种增长呢？我这里介绍一种“双向广度优先搜索”。它巧妙地运用了两个方向的广度优先搜索，大幅降低了搜索的度数。

15丨从树到图：如何让计算机学会看地图？

使用Dijkstra算法来查找地图中两点之间的最短路径。

16丨时间和空间复杂度（上）：优化性能是否只是“纸上谈兵”？

17丨时间和空间复杂度（下）：如何使用六个法则进行复杂度分析？

18丨总结课：数据结构、编程语句和基础算法体现了哪些数学思想？

04-概率统计篇 (14讲)

19丨概率和统计：编程为什么需要概率和统计？

20丨概率基础（上）：一篇文章帮你理解随机变量、概率分布和期望值

随机变量

概率分布

  1. 离散概率分布：伯努利分布、分类分布、二项分布、泊松分布
    1. 伯努利分布：二分类分布
    2. 分类分布：随机变量的取值空间为n个离散的值，n=2时就是伯努利分布。
  2. 连续概率分布：正态分布、均匀分布、指数分布、拉普拉斯分布
    1. 正态分布：也叫高斯分布，有两个关键参数：均值和方差。

期望值

均值是期望值的特例，即各个取值的概率相同。

21丨概率基础（下）：联合概率、条件概率和贝叶斯法则，这些概率公式究竟能做什么？

联合概率

由多个随机变量决定的概率我们就叫联合概率，使用P(x, y)表示。

边缘概率

联合概率和单个随机变量的概率之间有什么关联呢？对于离散型随机变量，我们可以通过通过联合概率P(x, y)在y上求和，就可以得到P(x)。对于连续型随机变量，我们可以通过联合概率P(x, y)在y上的积分，推导出概率P(x)。这个时候，我们称P(x)为边缘概率。

条件概率

条件概率也是由多个随机变量决定，但是和联合概率不同的是，它计算了给定某个（或多个）随机变量的情况下，另一个（或多个）随机变量出现的概率，其概率分布叫做条件概率分布。给定随机变量x，随机变量y的条件概率使用P(y|x)表示。

贝叶斯法则

条件概率、联合概率之间的关系如下： P(x,y) = P(x|y) * P(y)

根据上面的关系，可以得到贝叶斯定理如下：

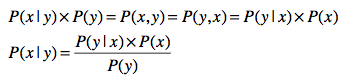
20220531贝叶斯定理.png

  1. 先验概率： 我们把P(x)称为先验概率。之所以称为“先验”，是因为它是从数据资料统计得到的，不需要经过贝叶斯定理的推算。
  2. 条件概率（似然函数）：P(y|x)是给定x之后y出现的条件概率。在统计学中，我们也把P(y|x)写作似然函数L(x|y)。在数学里，似然函数和概率是有区别的。概率是指已经知道模型的参数来预测结果，而似然函数是根据观测到的结果数据，来预估模型的参数。不过，当y值给定的时候，两者在数值上是相等的，在应用中我们可以不用细究。
  3. 边缘概率：我们没有必要事先知道P(y)。P(y)可以通过联合概率P(x,y)计算边缘概率得来，而联合概率P(x,y)可以由P(y|x)*P(x)推出。
  4. 后验概率：P(x|y)是根据贝叶斯定理，通过先验概率P(x)、似然函数P(y|x)和边缘概率P(y)推算而来，因此我们把它称作后验概率。

如果有一定数量的标注数据，那么通过统计的方法，我们可以很方便地得到先验概率和似然函数，然后推算出后验概率，最后依据后验概率来做预测。这整个过程符合监督式机器学习的模型训练和新数据预测这两个阶段，因此朴素贝叶斯算法被广泛运用在机器学习的分类问题中。

随机变量之间的独立性

如果随机变量x和y之间不相互影响，那么我们就说x和y相互独立。此时，有P(x|y)=P(x)，所以P(x,y)=P(x)*P(y)。

变量之间的独立性，可以帮我们简化计算。

举个例子，假设有6个随机变量，而每个变量有10种可能的取值，那么计算它们的联合概率p(x1,x2,x3,x4,x5,x6)，在实际中是非常困难的一件事情。

根据排列，可能的联合取值，会达到10的6次方，也就是100万这么多。那么使用实际的数据进行统计时，我们也至少需要这个数量级的样本，否则的话很多联合概率分布的值就是0，产生了数据稀疏的问题。但是，如果假设这些随机变量都是相互独立的，那么我们就可以将联合概率p(x1,x2,x3,x4,x5,x6)转换为p(x1)*p(x2)*p(x3)*p(x4)*p(x5)*p(x6)。如此一来，我们只需要计算p(x1)到p(x6)就行了。

22丨朴素贝叶斯：如何让计算机学会自动分类？

训练样本

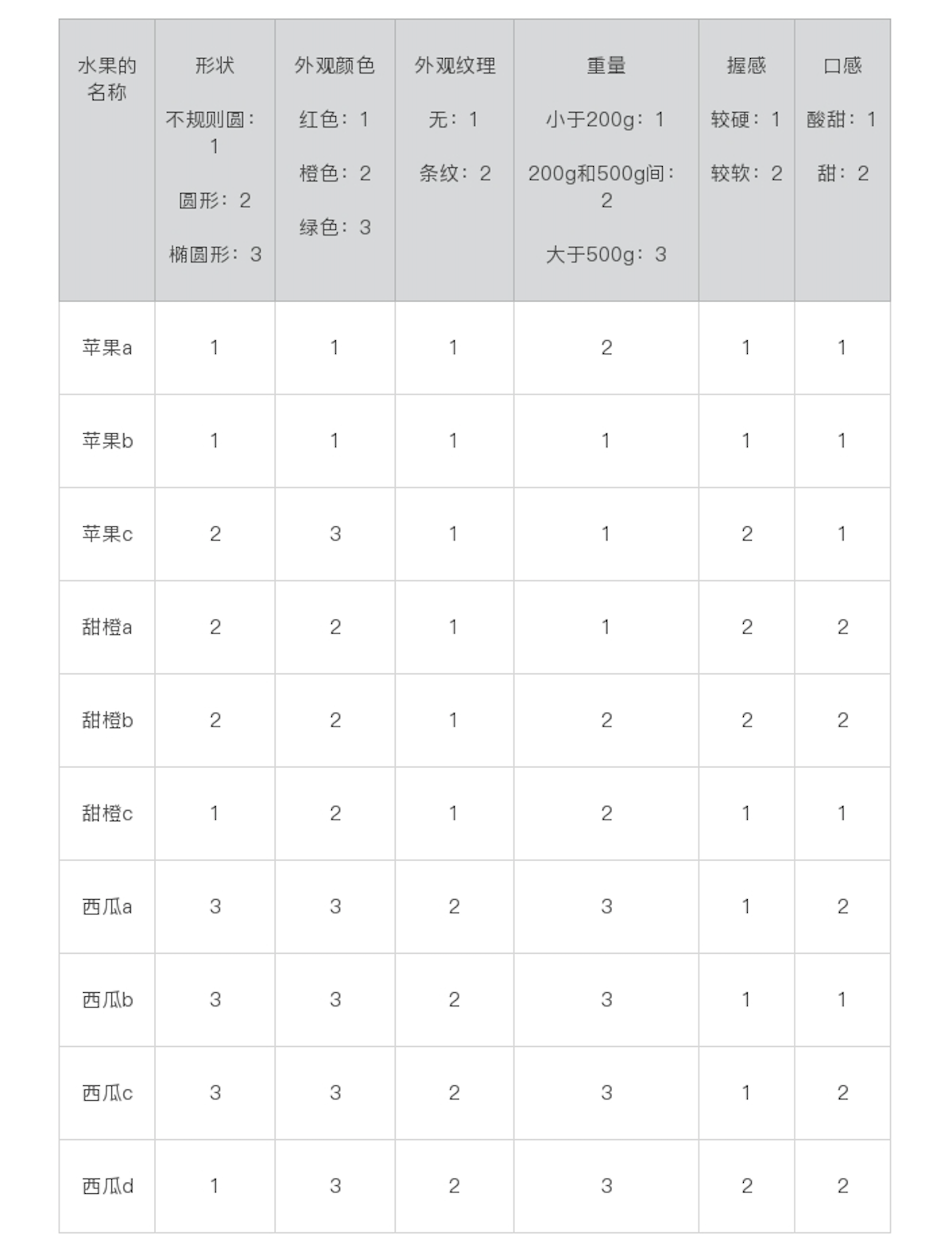
贝叶斯分类需要的训练样本如下： 20220531训练样本

训练

贝叶斯定理的核心思想：用先验概率和条件概率估计后验概率。

具体到这里的分类问题，贝叶斯公式可以写成这样：

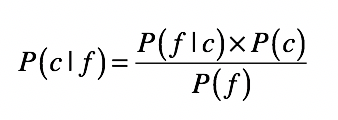
20220531贝叶斯分类公式.png

其中c表示一个分类（class）, f表示属性对应的数据字段（field）。如此一来，等号左边的P(c|f)就是待分类样本中，出现属性值f时，样本属于类别c的概率。而等号右边的P(f|c)是根据训练数据统计，得到分类c中出现属性f的概率。P(c)是分类c在训练数据中出现的概率，P(f)是属性f在训练样本中出现的概率。

这里的贝叶斯公式只描述了单个属性值属于某个分类的概率，可是我们要分析的水果每个都有很多属性，朴素贝叶斯在这里就要发挥作用了。这是基于一个简单假设建立的一种贝叶斯方法，并假定数据对象的不同属性对其归类影响时是相互独立的。此时若数据对象o中同时出现属性fi与fj，则对象o属于类别c的概率就是这样：

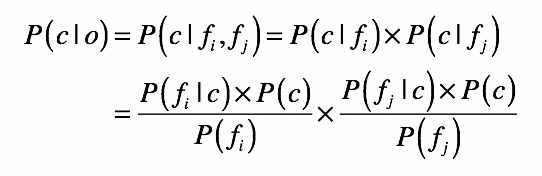
20220531朴素贝叶斯分类公式.png

现在，我们应该已经可以用10个水果的数据，来建立朴素贝叶斯模型了。

比如，苹果的分类中共包含3个数据实例，对于形状而言，出现2次不规则圆、1次圆形和0次椭圆形，因此各自的统计概率为0.67、0.33和0.00。我们将这些值称为，给定一个水果分类时，出现某个属性值的条件概率。以此类推，所有的统计结果就是下面这个表格中这样：

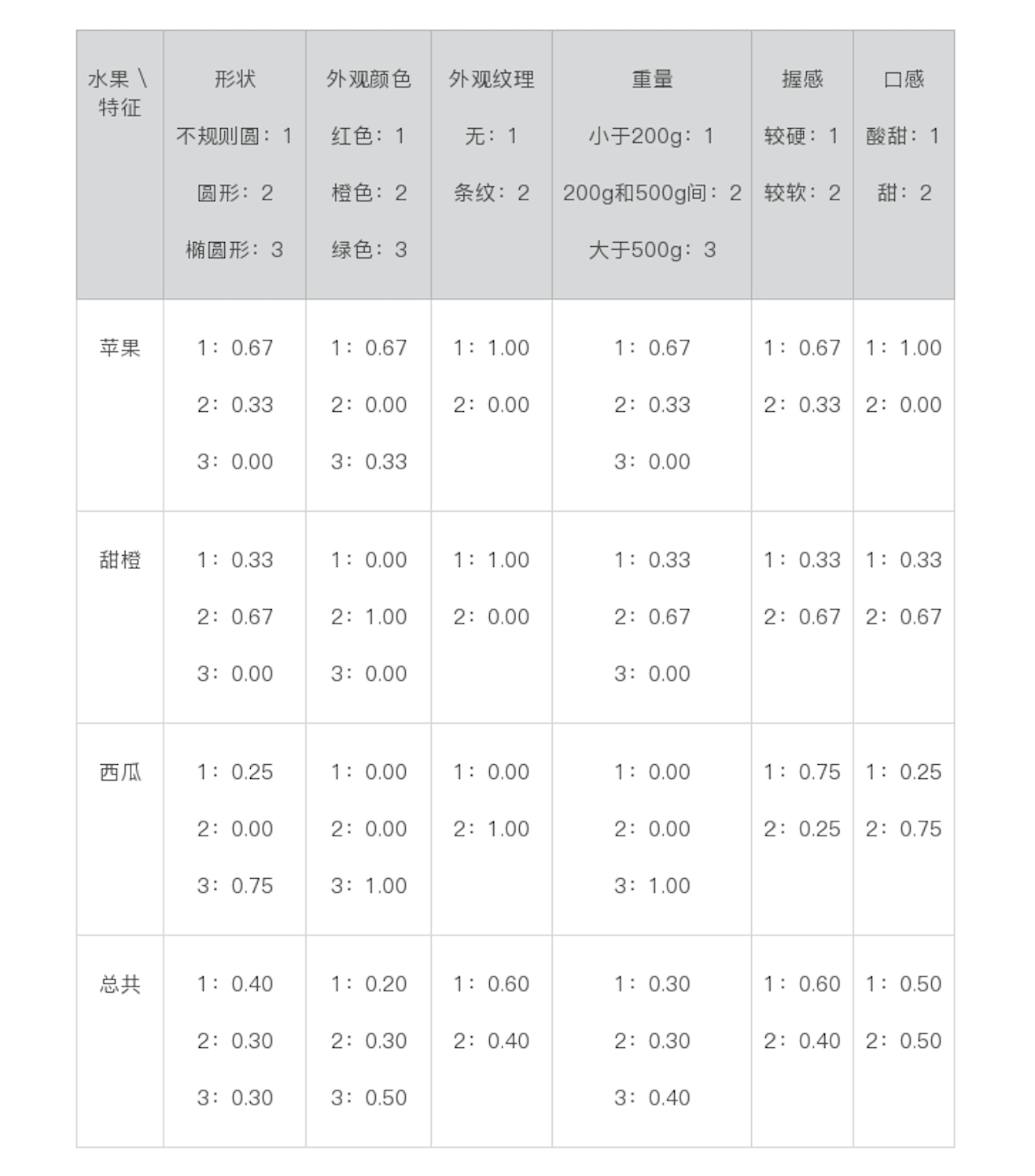
20220531贝叶斯训练样本条件概率.png

对于上表中出现的0.00概率，在做贝叶斯公式中的乘积计算时，会出现结果为0的情况，因此我们通常取一个比这个数据集里最小统计概率还要小的极小值，来代替“零概率”。比如，我们这里取0.01。在填充训练数据中从来没有出现过的属性值的时候，我们就会使用这种技巧，我们给这种技巧起个名字就叫作平滑（Smoothing）。

预测

有了这些条件概率，以及各类水果和各个属性出现的先验概率，我们已经建立起了朴素贝叶斯模型。现在，我们就可以用它进行朴素贝叶斯分类了。

假设我们有一个新的水果，它的形状是圆形，口感是甜的，那么根据朴素贝叶斯，它属于苹果、甜橙和西瓜的概率分别是多少呢？

我们先来计算一下，它属于苹果的概率有多大:

20220531贝叶斯分类预测苹果概率.png

其中，apple表示分类为苹果，shape-2表示形状属性的值为2（也就是圆形），taste-2表示口感属性的值为2。以此类推，我们还可计算该水果属于甜橙和西瓜的概率:

20220531贝叶斯分类预测橙子西瓜概率.png

比较这三个数值，0.00198<0.00798<0.26934，所以计算机可以得出的结论，该水果属于甜橙的可能性是最大的，或者说，这个水果最有可能是甜橙。

这几个公式里的概率乘积通常都非常小，在物品的属性非常多的时候，这个乘积可能就小到计算机无法处理的地步。因此，在实际运用中，我们还会采用一些数学手法进行转换（比如取log将小数转换为绝对值大于1的负数），原理都是一样的。

总结

总结一次朴素贝叶斯分类的主要步骤：

  1. 准备数据：针对水果分类这个案例，我们收集了若干水果的实例，并从水果的常见属性入手，将其转化为计算机所能理解的数据。这种数据也被称为训练样本。
  2. 建立模型：通过手头上水果的实例，我们让计算机统计每种水果、属性出现的先验概率，以及在某个水果分类下某种属性出现的条件概率。这个过程也被称为基于样本的训练。
  3. 分类新数据：对于一颗新水果的属性数据，计算机根据已经建立的模型进行推导计算，得到该水果属于每个分类的概率，实现了分类的目的。这个过程也被称为预测。

23丨文本分类：如何区分特定类型的新闻？

运用朴素贝叶斯原理，根据词频特征，对文章进行分类。清晰明了，值得一看。

24丨语言模型：如何使用链式法则和马尔科夫假设简化概率模型？

语言模型

这里说的语言模型指的是基于概率和统计的语言模型。

链式法则

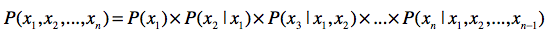
20220531链式法则.png

马尔可夫假设

理解了链式法则，我们再来看看马尔可夫假设。这个假设的内容是：任何一个词wi出现的概率只和它前面的1个或若干个词有关。基于这个假设，我们可以提出多元文法（Ngram）模型。Ngram中的N很重要，它表示任何一个词出现的概率，只和它前面的N-1个词有关。

以二元文法模型为例，按照刚才的说法，二元文法表示，某个单词出现的概率只和它前面的1个单词有关。也就是说，即使某个单词出现在一个很长的句子中，我们也只需要看前面那1个单词。用公式来表示出来就是这样：

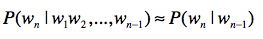
20220531二元文法模型.png

假设我们有一个统计样本文本d，s表示某个有意义的句子，由一连串按照特定顺序排列的词w1，w2,…,wn组成，这里n是句子里单词的数量。现在，我们想知道根据文档d的统计数据，s在文本中出现的可能性，即P(s|d)，那么我们可以把它表示为P(s|d)=P(w1,w2,…,wn|d)。假设我们这里考虑的都是在集合d的情况下发生的概率，所以可以忽略d，写为P(s)=P(w1,w2,…,wn)。

P(w1,w2,…,wn)可以通过上面说的链式法则计算，通过文档集合C，你可以知道P(w1)，P(w2|w1)这种概率。但是，这会带来两个问题：

  1. 概率为0的问题 P(w1)大小还好，P(w2|w1)会小一些，再往后看，P(w3|w1,w2)出现概率更低，P(w4|w1,w2,w3)出现的概率就更低了。一直到P(wn|w1,w2,…,wn−1)，基本上又为0了。我们可以使用上一节提到的平滑技巧，减少0概率的出现。不过，如果太多的概率都是通过平滑的方式而得到的，那么模型和真实的数据分布之间的差距就会加大，最终预测的效果也会很差，所以平滑也不是解决0概率的最终办法。
  2. 存储空间的问题 为了统计现有文档集合中P(w1,w2,…,wn)这类值，我们就需要生成很多的计数器。我们假设文档集合中有m个不同的单词，那么从中挑出n个单词的可重复排列，数量就是m^n。此外，还有m^(n−1),m^(n−2)等等。这也意味着，如果要统计并存储的所有P(w1,w2,…,wn)或P(wn|w1,w2,…,wn−1)这类概率，就需要大量的内存和磁盘空间。当然，你可以做一些简化，不考虑单词出现的顺序，那么问题就变成了可重复组合，但是数量仍然非常巨大。

在这两个问题上，马尔科夫假设和多元文法模型就能帮上大忙了。如果我们使用三元文法模型，上述公式可以改写为：

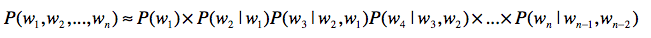
20220531三元文法模型.png

这样，系统的复杂度大致在(C(m,1)+C(m,2)+C(m,3))这个数量级，而且P(wn|wn−2,wn−1)为0的概率也会大大低于P(wn|w1,w2,…,wn−1)为0的概率。

语言模型的应用

基于概率的语言模型，本身不是新兴的技术。它已经在机器翻译、语音识别和中文分词中得到了成功应用。近几年来，人们也开始在信息检索领域中尝试语言模型。下面我就来讲讲语言模型在信息检索和中文分词这两个方面里是如何发挥作用的。

信息检索

信息检索很关心的一个问题就是相关性，也就是说，给定一个查询，哪篇文档是更相关的呢？一种常见的做法是计算P(d|q)，其中q表示一个查询，d表示一篇文档。P(d|q)表示用户输入查询q的情况下，文档d出现的概率是多少？如果这个概率越高，我们就认为q和d之间的相关性越高。

通过我们手头的文档集合，并不能直接获得P(d|q)。好在我们已经学习过了贝叶斯定理，通过这个定理，我们可以将P(d|q)重写如下：

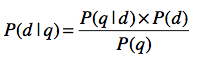
20220531信息检索贝叶斯公式.png

让k1,k2,…,kn表示查询q里包含的n个关键词，就可以根据链式法则求解出P(q|d)，我们也使用马尔科夫假设和多元文法来提高算法效率。

最终，当用户输入一个查询q之后，对于每一篇文档d，我们都能获得P(d|q)的值。根据每篇文档所获得的P(d|q)这个值，由高到低对所有的文档进行排序。这就是语言模型在信息检索中的常见用法。

中文分词

和拉丁语系不同，中文存在分词的问题。比如原句是“兵乓球拍卖完了”，分词结果可能是：

1
2
3

1. 兵乓球|拍卖|完了
2. 兵乓|球拍|卖完|了
3. ...

上面分词的例子，从字面来看都是合理的，所以这种歧义无法通过这句话本身来解决。那么这种情况下，语言模型能为我们做什么呢？我们知道，语言模型是基于大量的语料来统计的，所以我们可以使用这个模型来估算，哪种情况更合理。

假设整个文档集合是D，要分词的句子是s，分词结果为w1,…wn，如果使用三元文法模型，

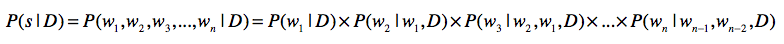
20220531中文分词三元文法模型.png

请注意，在信息检索中，我们关心的是每篇文章产生一个句子（也就是查询）的概率，而这里可以是整个文档集合D产生一个句子的概率。

语言模型可以帮我们估计某种分词结果，在文档集合中出现的概率。由于不同的分词方法，会导致w1到wn的不同，因此就会产生不同的P(s)。接下来，我们只要取最大的P(s)，并假设这种分词方式是最合理的，就可以在一定程度上解决歧义。

回到“兵乓球拍卖完了”这句话，如果文档集合都是讲述的有关体育用品的销售，而不是拍卖行，那么“兵乓|球拍|卖完|了”这种分词的可能性应该更高。

25丨马尔科夫模型：从PageRank到语音识别，背后是什么模型在支撑？

马尔可夫模型

在介绍语言模型的时候，我们提到了马尔科夫假设，这个假设是说，每个词出现的概率和之前的一个或若干个词有关。我们换个角度思考就是，每个词按照一定的概率转移到下一个词。

如果把词抽象为一个状态，那么我们就可以认为，状态到状态之间是有关联的。前一个状态有一定的概率可以转移到到下一个状态。如果多个状态之间的随机转移满足马尔科夫假设，那么这类随机过程就是一个马尔科夫随机过程。而刻画这类随机过程的统计模型，就是马尔科夫模型（Markov Model）。

前面讲多元文法的时候，我提到了二元文法、三元文法。对于二元文法来说，某个词出现的概率只和前一个词有关。对应的，在马尔科夫模型中，如果一个状态出现的概率只和前一个状态有关，那么我们称它为一阶马尔科夫模型或者马尔科夫链。对应于三元、四元甚至更多元的文法，我们也有二阶、三阶等马尔科夫模型。

PageRank和马尔可夫链

Google公司最引以为傲的PageRank链接分析算法，它的核心思想就是基于马尔科夫链。这个算法假设了一个“随机冲浪者”模型，冲浪者从某张网页出发，根据Web图中的链接关系随机访问。在每个步骤中，冲浪者都会从当前网页的链出网页中随机选取一张作为下一步访问的目标。在整个Web图中，绝大部分网页节点都会有链入和链出。那么冲浪者就可以永不停歇地冲浪，持续在图中走下去。我们可以假设每张网页就是一个状态，而网页之间的链接表明了状态转移的方向。这样，我们很自然地就可以使用马尔科夫链来刻画“随机冲浪者”。

  1. PageRank值：在随机访问的过程中，越是被频繁访问的链接，越是重要。可以看出，每个节点的PageRank值取决于Web图的链接结构。假如一个页面节点有很多的链入链接，或者是链入的网页有较高的被访问率，那么它也将会有更高的被访问概率。
  2. PageRank在标准的马尔科夫链上，引入了随机的跳转操作，也就是假设冲浪者不按照Web图的拓扑结构走下去，只是随机挑选了一张网页进行跳转。这样的处理是类比人们打开一张新网页的行为，也是符合实际情况的，避免了信息孤岛的形成。

    隐马尔可夫模型

    马尔可夫模型都是假设每个状态对我们都是已知的，比如在概率语言模型中，一个状态对应了单词“上学”，另一个状态对应了单词“书包”。可是，有没有可能某些状态我们是未知的呢？

在某些现实的应用场景中，我们是无法确定马尔科夫过程中某个状态的取值的。这种情况下，最经典的案例就是语音识别。使用概率对语音进行识别的过程，和语言模型类似，因此我们可以把每个等待识别的词对应为马尔科夫过程中的一个状态。

计算机只知道某个词的发音，而不知道它具体怎么写，对于这种情况，我们就认为计算机只能观测到每个状态的部分信息，而另外一些信息被“隐藏”了起来。这个时候，我们就需要用隐马尔科夫模型来解决这种问题。隐马尔科夫模型有两层，一层是我们可以观测到的数据，称为“输出层”，另一层则是我们无法直接观测到的状态，称为“隐藏状态层”。如下图：

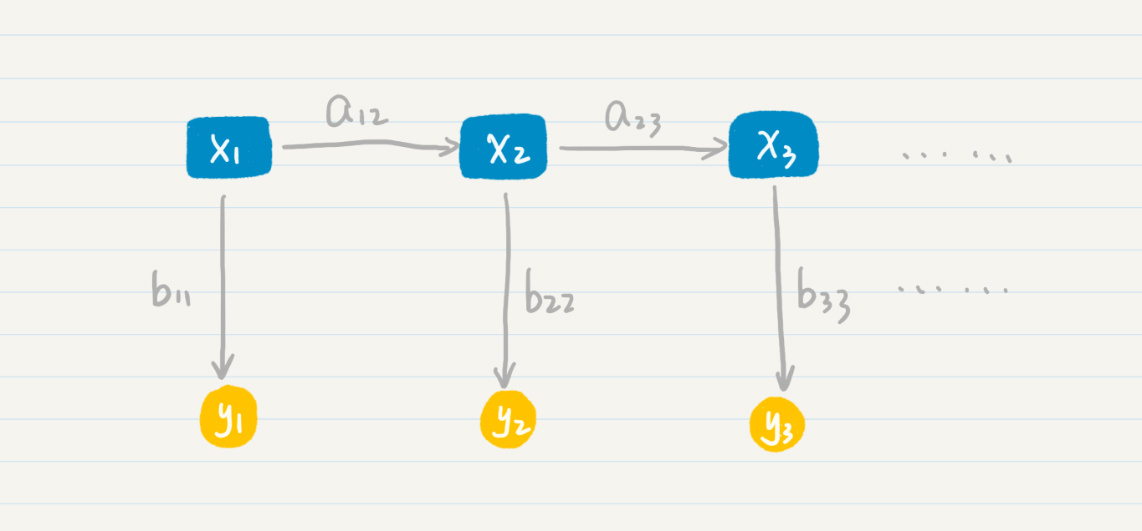
20220531隐马尔可夫模型图.jpeg

那么在这个两层模型示例中，“隐藏状态层”(x1，x2，x3)产生“输出层”(y1，y2，y3)的概率是:

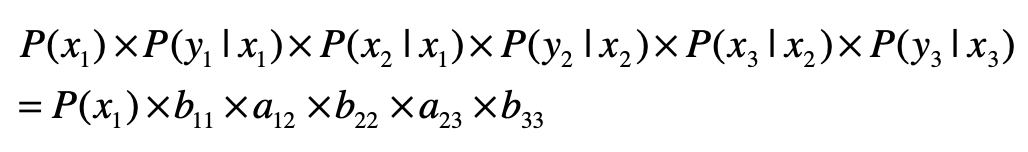
20220531隐马尔可夫模型输出层概率.png

语音识别要做的，就是遍历所有可能的状态层，找出最可能产生已知“输出层”的状态层，即为语音识别结果。

26丨信息熵：如何通过几个问题，测出你对应的武侠人物？

现在有个小游戏，“测测你是哪个武侠人物”：通过连续的几个问题，确定答题者是武侠人物中的哪一位？

那么，问卷设计者应该如何选择合适的题目，才能在读者回答尽量少的问题的同时，相对准确地测出自己对应于武侠中的哪个人物呢？为了实现这一目的，系统背后需要有这样的一张表格：

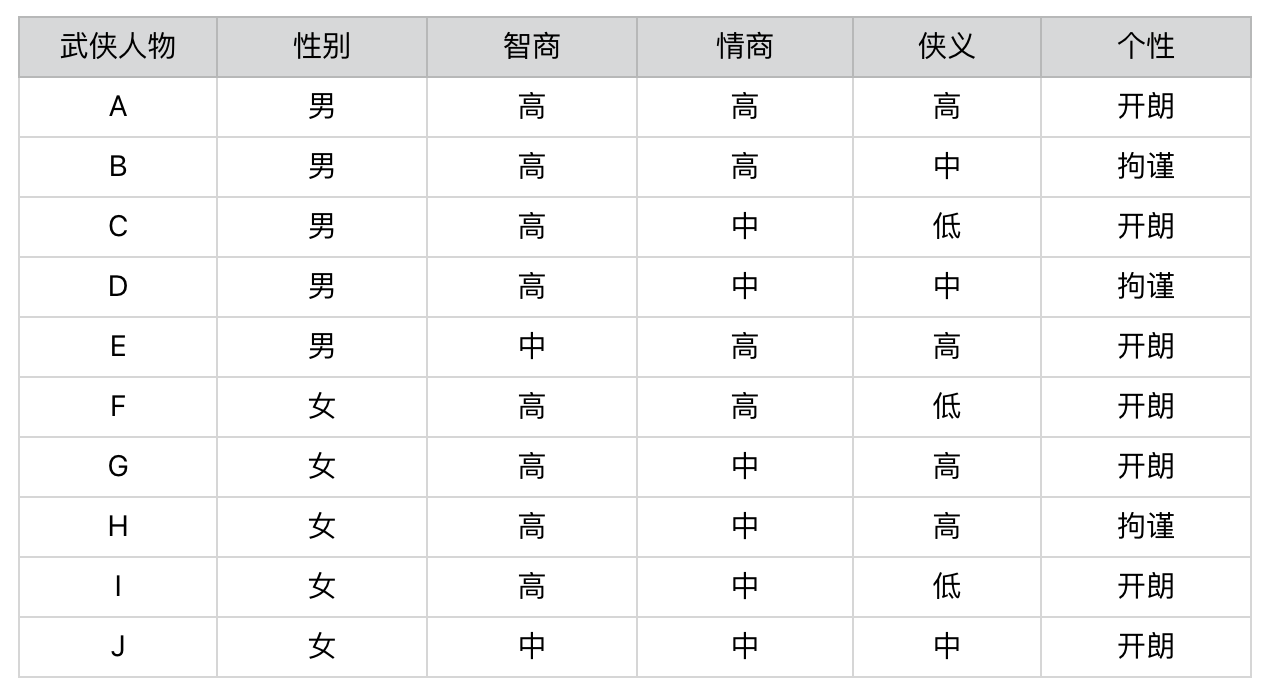
20220531信息熵游戏表格.png

在题目的设计上，我们可能要考虑下面两个问题： 1. 每个问题在人物划分上，是否有着不同的区分能力？ 2. 题目的先后顺序会不会直接影响要回答问题的数量？

问题的区分能力

每一个问题都会将被测试者划分为不同的人物分组。如果某个问题将属于不同人物分组的被测者，尽可能地划分到了相应的分组，那么我们认为这个问题的区分能力较强。相反，如果某个问题无法将属于不同人物分组的被测者划分开来，那么我们认为这个问题的区分能力较弱。

举个例子，我们先来比较一下“性别”和“智商”这两个属性。

首先，性别属性将武侠人物平均地划分为一半一半，也就是说“男”和“女”出现的先验概率是各 50%。如果我们假设被测试的人群，其男女性别的概率分布也是50%和50%，那么关于性别的测试题，就能将被测者的群体大致等分。

我们再来看智商属性。我们也将武侠人物划分为2个小集合，不过“智商高”的先验概率是 80%，而“智商中等”的先验概率只有 20%。同样，我们假设被测试的人群，其智商的概率分布也是类似地，那么经过关于智商的测试题之后，仍然有 80% 左右的不同人物还是属于同一个集合，并没有被区分开来。因此，我们可以认为关于“智商”的测试题，在对人物进行分组这个问题上，其能力要弱于“性别”的测试题。

这只是对区分能力的一个感性认识，如何对其进行量化呢？这就需要引入信息量，信息熵，信息增益等概念。

信息量

任何能够减少不确定性的消息，都叫做信息。定性地看，事件的概率越小，不确定性越大，一旦发生带来的信息量也就越大。信息量公式如下：

20220531信息量公式.svg

信息熵

一个系统的信息熵是其各种状态的信息量的期望：

20220531信息熵公示.svg

这个公式和热力学的熵的本质一样，故也称为熵。从公式可知，当各个符号出现的几率相等，即“不确定性”最高时，信息熵最大。故信息可以视为“不确定性”、“不纯净度”或“选择的自由度”的度量。

从集合和分组的角度来说，如果一个集合里的元素趋向于落在同一分组里，那么告诉你某个元素属于哪个分组的信息量就越小，整个集合的熵也越小，换句话说，整个集合就越“纯净”。相反，如果一个集合里的元素趋向于分散在不同分组里，那么告诉你某个元素属于哪个分组的信息量就越大，整个集合的熵也越大，换句话说，整个集合就越“混乱”。

已经知道单个集合的熵是如何计算的了。那么，如果将一个集合划分成多个更小的集合之后，又该如何根据这些小集合，来计算整体的熵呢？之前我们提到了信息量和熵具有加和的性质，所以对于包含多个集合的更大集合，它的信息量期望值是可以通过每个小集合的信息量期望值来推算的。具体来说，我们可以使用如下公式：

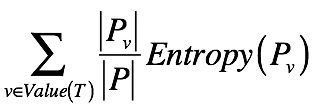
20220531集合划分信息熵公式.png

其中，T表示一种划分，Pv表示划分后其中某个小集合，Entropy(Pv)表示某个小集合的熵， 而|Pv|/|P|表示某个小集合出现的概率。

信息增益

一个系统的信息增益是指，由于信息量大增加带来的其信息熵的减少:

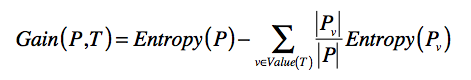
20220531信息增益公式.png

其中T表示当前选择的特征，Entropy(P)表示选择特征T之前的熵，Entropy(Pv)表示特征T取值为v分组的熵。减号后面的部分表示选择T做决策之后，各种取值子集合的熵的加权平均（期望）后整体的熵。

再次回到“武侠人物分类”的小游戏

我们把这个信息增益的概念放到咱们的小游戏里就是，如果一个测试问题能够将来自不同分组的人物尽量的分开，也就是该划分对应的信息增益越高，那么我们就认为其区分能力越高，提供的信息含量也越多。

我们还是以“性别”和“智商”的两个测试题为例。

在提出任何问题之前，我们无法知道被测者属于哪位武侠人物，因此所有被测者属于同一个集合。假设被测者的概率分布和这10位武侠人物的先验概率分布相同，那么被测者集合的熵为3.32(10*(-1 * 0.1 * log(0.1, 2)))。

通过性别的测试问题对人物进行划分后，我们得到了两个更小的集合，每个小集合都包含5种不同的人物分组，因此每个小集合的熵是2.32((-1 * 5 * 0.2 * log(0.2, 2)))，两个小集合的整体熵是2.32(0.5 * 2.32 + 0.5 * 2.32)。因此使用性格的测试题后，信息增益是1(3.32 - 2.32)。

而通过智商的测试问题对人物分组后，我们也得到了两个小集合，一个包含了8种人物，另一个包含了2种人物。包含8种人物的小集合其熵是3((-1* 8 * 0.125 * log(0.125, 2)))，包含2种人物的小集合其熵是1((-1* 2 * 0.5 * log(0.5, 2)))。两个小集合的整体熵是2.6(0.8 * 3 + 0.2 * 1)。因此使用智商的测试题后，信息增益是0.72(3.32 - 2.6)，低于基于性别的测试。所以，我们可以得出结论，有关性别的测试题比有关智商的测试题更具有区分能力。

27丨决策树：信息增益、增益比率和基尼指数的运用

继续“武侠人物分类”游戏

还说上面的“武侠人物分类”游戏，被测者们每次回答一道问题，就会被细分到不同的集合，每个细分的集合纯净度就会提高，而熵就会下降。在测试结束的时候，如果所有被测者都被分配到了相应的武侠人物名下，那么每个人物分组都是最纯净的，熵值都为0。于是，测试问卷的过程就转化为“如何将熵从3.32下降到0”的过程。

首先计算各个特征的信息增益：

20220531武侠人物游戏各个特征信息增益.png

按照信息增益从高到低的顺序选择特征问题：

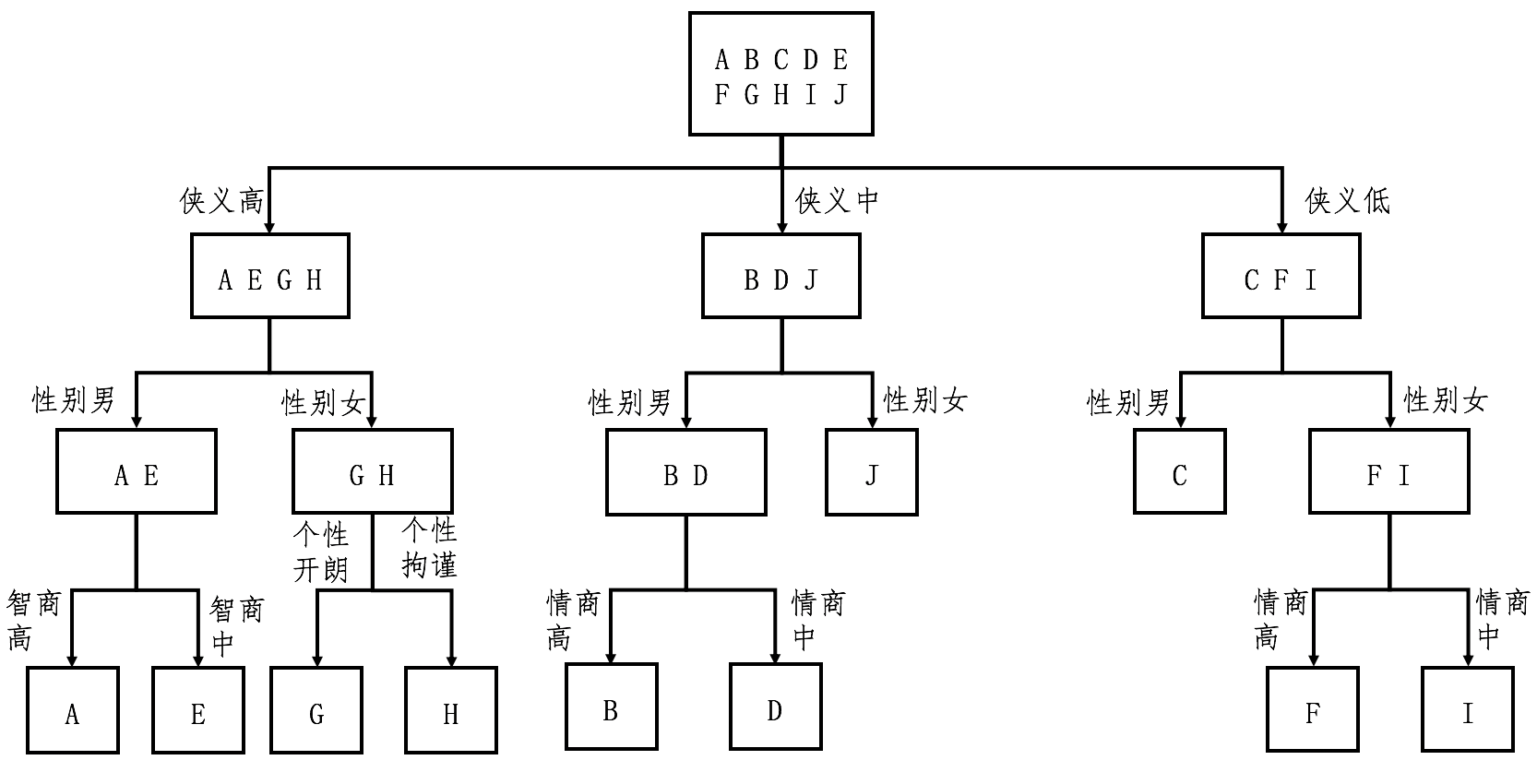
20220531武侠人物分类图.png

从这个图可以看出来，对于每种人物的判断，我们至多需要问3个问题，没有必要问全5个问题。比如，对于人物J和C，我们只需要问2个问题。假设读者属于10种武侠人物的概率是均等的，那么我们就可以利用之前介绍的知识，来计算读者需要回答的问题数量之期望值。每种人物出现的概率是0.1，8种人物需要问3个问题，2种人物需要问2个问题，那么回答问题数的期望值是2.8(0.8 * 3 + 0.2 * 2)。

如果我们每次不选熵值最高的问题，而选择熵值最低的问题，那么需要回答的问题的数量期望值为4到5之间。

决策树

上述这个过程就体现了训练决策树（Decision Tree）的基本思想。决策树学习属于归纳推理算法之一，适用于分类问题。决定问卷题出现顺序的这个过程，其实就是建立决策树模型的过程，即训练过程。

整个构建出来的图就是一个树状结构，这也是“决策树”这个名字的由来。而根据用户对每个问题的答案，从决策树的根节点走到叶子节点，最后来判断其属于何种人物类型，这个过程就是分类新数据的过程，即预测过程。

有点需要注意的是，问卷案例中的每类武侠人物。都只有一个样本，而在泛化的机器学习问题中，每个类型对应了多个样本。也就是说，我们可以有很多个郭靖，而且每个人的属性并不完全一致，但是它们的分类都是“郭靖”。正是因为这个原因，决策树通常都只能把整体的熵降低到一个比较低的值，而无法完全降到0。这也意味着，训练得到的决策树模型，常常无法完全准确地划分训练样本，只能求到一个近似的解。

几种常见的决策树算法

采用信息增益来构建决策树的算法被称为ID3（Iterative Dichotomiser 3，迭代二叉树3代）。但是这个算法有一个缺点，它一般会优先考虑具有较多取值的特征，因为取值多的特征会有相对较大的信息增益。这是为什么呢？

仔细观察一下信息熵的定义，就能发现背后的原因。更多的取值会把数据样本划分为更多更小的分组，这样熵就会大幅降低，信息增益就会大幅上升。但是这样构建出来的树，很容易导致机器学习中的过拟合现象，不利于决策树对新数据的预测。为了克服这个问题，人们又提出了一个改进版，C4.5算法。

决策树也有不足。这类算法受训练样本的影响很大，比较容易过拟合。在预测阶段，如果新的数据和原来的训练样本差异较大，那么分类效果就会比较差。为此人们也提出了一些优化方案，比如剪枝和随机森林。

28丨熵、信息增益和卡方：如何寻找关键特征？

通过信息增益进行特征选择

类似于决策树算法。

通过卡方检验进行特征选择

在统计学中，我们使用卡方检验来检验两个变量是否相互独立。把它运用到特征选择，我们就可以检验特征与分类这两个变量是否独立。如果两者独立，证明特征和分类没有明显的相关性，特征对于分类来说没有提供足够的信息量。反之，如果两者有较强的相关性，那么特征对于分类来说就是有信息量的，是个好的特征。

为了检验独立性，卡方检验考虑了四种情况的概率：P(fi,cj)、P(fi¯,cj¯)、P(fi,cj¯)和P(fi¯,cj)。

在这四种概率中，P(fi,cj)和P(fi¯,cj¯)表示特征fi和分类cj是正相关的。如果P(fi,cj)很高，表示特征fi的出现意味着属于分类cj的概率更高；如果P(fi¯,cj¯)很高，表示特征fi不出现意味着不属于分类cj的概率更高。

类似地，P(fi,cj¯)和P(fi¯,cj)表示特征fi和分类cj是负相关的。如果P(fi,cj¯)很高，表示特征fi的出现意味着不属于分类cj的概率更高；如果P(fi¯,cj)很高，表示特征fi不出现意味着属于分类cj的概率更高。

如果特征和分类的相关性很高，要么是正向相关值远远大于负向相关值，要么是负向相关值远远大于正向相关值。如果特征和分类相关性很低，那么正向相关值和负向相关的值就会很接近。卡方检验就是利用了正向相关和负向相关的特性。

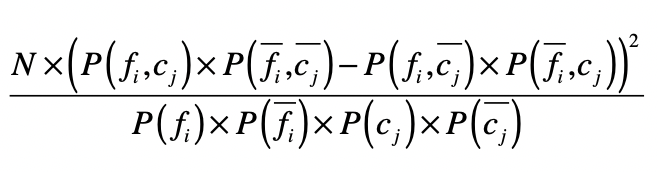
20220531卡方检验进行特征选择.png

其中，N表示数据的总个数。通过这个公式，你可以看到，如果一个特征和分类的相关性很高，无论是正向相关还是负向相关，那么正向相关和负向相关的差值就很大，最终计算的值就很高。最后，我们就可以按照卡方检验的值由高到低对特征进行排序，挑选出排列靠前的特征。

29丨归一化和标准化：各种特征如何综合才是最合理的？

第一点，为什么有时候需要转换特征值？因为不同类型的特征取值范围不同，分布也不同，相互之间没有可比性。因此在线性回归中，通过这些原始值分析得到的权重，并不能代表每个特征实际的重要性。

我们用Boston Housing 数据集对房价数据进行回归分析，这个数据来自 70 年代美国波斯顿周边地区的房价，是用于机器学习的经典数据集，你可以在Kaggle的网站下载到它，并查看表格中各列的含义：

  1. CRIM：per capita crime rate by town.
  2. ZN：proportion of residential land zoned for lots over 25,000 sq.ft.
  3. INDUS：proportion of non-retail business acres per town.
  4. CHAS：Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
  5. NOX：nitrogen oxides concentration (parts per 10 million).
  6. RM：average number of rooms per dwelling.
  7. AGE：proportion of owner-occupied units built prior to 1940.
  8. DIS：weighted mean of distances to five Boston employment centres.
  9. RAD：index of accessibility to radial highways.
  10. TAX：full-value property-tax rate per \$10,000.
  11. PTRATIO：pupil-teacher ratio by town.
  12. B：1000(Bk - 0.63)2 where Bk is the proportion of blacks by town.
  13. LSTAT：lower status of the population (percent).
  14. MEDV：median value of owner-occupied homes in \$1000s.

Kaggle上面好像不能直接下载啦，可以点击这里下载。

使用下面的python代码实现线性回归分析：

1
2
3
4
5
6
7
8
9
10

import pandas as pd
from sklearn.linear_model import LinearRegression

df = pd.read_csv("demo/datasets/boston_house_price.csv")  # 读取 Boston Housing 中的 csv数据
df_features = df.drop(['MEDV'], axis=1)  # Dataframe 中除了最后一列，其余列都是特征，或者说自变量
df_targets = df['MEDV']  # Dataframe 最后一列是目标变量，或者说因变量
#
regression = LinearRegression().fit(df_features, df_targets)  # 使用特征和目标数据，拟合线性回归模型
print(regression.score(df_features, df_targets))  # 拟合程度的好坏
print(regression.coef_)  # 各个特征所对应的系

输出结果：

1
2
3
4
5

0.7406426641094095
[-1.08011358e-01  4.64204584e-02  2.05586264e-02  2.68673382e+00
 -1.77666112e+01  3.80986521e+00  6.92224640e-04 -1.47556685e+00
  3.06049479e-01 -1.23345939e-02 -9.52747232e-01  9.31168327e-03
 -5.24758378e-01]

因为不是所有的数据都是可以使用线性回归模型来表示，所以我们需要使用 regression.score 函数，来看拟合的程度。如果完美拟合，这个函数就会输出 1；如果拟合效果很差，这个函数的输出可能就是一个负数。

这里 regression.score 函数的输出大约为 0.74，接近于 1.0。它表示这个数据集使用线性模型拟合的效果还是不错的。

注意：下面是原文章中的解释，但是和我下载到的数据跑出的结果匹配不上，但是有关归一化和标准化的作用还是能够看出来的。 原文章中的输出：

1
2
3
4
5

0.735578647853312
[-4.54789253e-03 -5.17062363e-02  4.93344687e-02  5.34084254e-02
  3.78011391e+00 -1.54106687e+01  3.87910457e+00 -9.51042267e-03
 -1.60411361e+00  3.61780090e-01 -1.14966409e-02 -8.48538613e-01
  1.18853164e-02 -6.01842329e-01]

权重可以帮助我们解释哪个特征对最终房价的中位值有更大的影响。参看 csv 中的数据，你会发现最主要的两个正相关特征是 nox（系数为 3.78011391e+00）和 age（系数为 3.87910457e+00）。其中 nox 表示空气污染浓度，age 表示老房子占比，也就是说空气污染越多、房龄越高，房价中位数越高，这好像不太合乎常理。我们再来看看最主要的负相关特征 rm（系数为 -1.54106687e+01），也就是房间数量。房间数量越多，房价中位数越低，也不合理。

造成这些现象最重要的原因是，不同类型的特征值没有转换到同一个可比较的范围内，所以线性回归后所得到的系数不具有可比性，因此我们无法直接对这些权重加以解释。

归一化（Normalization）

简单起见，这里的归一化是指使用特征取值范围中的最大值和最小值，把原始值转换为0到1之间的值。这样处理的好处在于简单易行，便于理解。不过，它的缺点也很明显，由于只考虑了最大最小值，因此很容易受到异常数据点的干扰。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler

minMaxScaler = MinMaxScaler()  # 基于 min 和 max 值的归一化

df = pd.read_csv("demo/datasets/boston_house_price.csv")  # 读取 Boston Housing 中的 csv的数据
df_normalized = minMaxScaler.fit_transform(df)  # 对原始数据进行归一化，包括特征值和目标变量
df_features_normalized = df_normalized[:, 0:-1]  # 获取归一化之后的特征值
df_targets_normalized = df_normalized[:, -1]  # 获取归一化之后的目标值

# 再次进行线性回归
regression_normalized = LinearRegression().fit(df_features_normalized, df_targets_normalized)
print(regression_normalized.score(df_features_normalized, df_targets_normalized))
print(regression_normalized.coef_)

输出：

1
2
3
4

0.7406426641094094
[-0.21355017  0.10315657  0.0124631   0.0597052  -0.1918794   0.4418597
  0.00149367 -0.36059247  0.15642529 -0.14362949 -0.19901831  0.08206283
 -0.42260541]

注意：下面是原文章中的解释，但是和我下载到的数据跑出的结果匹配不上，但是有关归一化和标准化的作用还是能够看出来的。 原文章中的输出：

1
2
3
4

0.7355786478533118
[-0.05103746 -0.08448544  0.10963215  0.03204506  0.08400253 -0.16643522
  0.4451488  -0.01986622 -0.34152292  0.18490982 -0.13361651 -0.16216516
  0.10390408 -0.48468369]

你可以看到，表示拟合程度的分数没有变，但是每个特征对应的系数或者说权重，发生了比较大的变化。仔细观察一下，你会发现，这次最主要的正相关特征是 age（0.4451488）和 tax（0.18490982），也就是老房子占比和房产税的税率，其中至少房产税的税率是比较合理的，因为高房价的地区普遍税率也比较高。而最主要的负相关特征是 rad（-0.34152292）和 lstat（-0.48468369），rad 表示高速交通的便利程度，它的值越大表示离高速越远，房价中位数越低。而 lstat 表示低收入人群的占比，这个值越大房价中位数越低，这两点都是合理的。

标准化（Standardizaiton）

另一种常见的方法是基于正态分布的 z 分数（z-score）标准化（Standardization）。该方法假设数据呈现标准正态分布。

经过标准化处理之后，每种特征的取值都会变成一个标准正态分布，以0为均值，1为标准差。和归一化相比，标准化使用了数据是正态分布的假设，不容易受到过大或过小值的干扰。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

standardScaler = StandardScaler()  # 基于 Z 分数的标准化

df = pd.read_csv("demo/datasets/boston_house_price.csv")  # 读取 Boston Housing 中的 csv的数据
print(df)
standardScaler.fit(df)
df_standardized = standardScaler.transform(df)  # 对原始数据进行标准化，包括特征值和目标变量
print(df_standardized)

df_features_standardized = df_standardized[:, 0:-1]  # 获取标准化之后的特征值
df_targets_standardized = df_standardized[:, -1]  # 获取标准化之后的特征值

# 再次进行线性回归
regression_standardized = LinearRegression().fit(df_features_standardized, df_targets_standardized)
print(regression_standardized.score(df_features_standardized, df_targets_standardized))
print(regression_standardized.coef_)

输出：

1
2
3
4

0.7406426641094093
[-0.10101708  0.1177152   0.0153352   0.07419883 -0.22384803  0.29105647
  0.00211864 -0.33783635  0.28974905 -0.22603168 -0.22427123  0.09243223
 -0.40744693]

注意：下面是原文章中的解释，但是和我下载到的数据跑出的结果匹配不上，但是有关归一化和标准化的作用还是能够看出来的。 原文章中的输出：

1
2
3
4

0.7355786478533118
[-0.07330367 -0.04144107  0.12194378  0.04074345  0.09805446 -0.19311408
  0.29767387 -0.02916672 -0.34642803  0.34477088 -0.21410757 -0.19904179
  0.11218058 -0.46369483]

表示拟合程度的分数任然没有变。再次对比不同特征所对应的系数，你会发现这次最主要的正相关特征还是 age（0.29767387）和 tax（0.34477088），但是相比之前，明显房产税的税率占了更高的权重，更加合理。而最主要的负相关特征还是 rad（-0.34152292）和 lstat（-0.48468369），这两点都是合理的。

30丨统计意义（上）：如何通过显著性检验，判断你的A-B测试结果是不是巧合？

  1. 显著性差异
  2. 统计假设检验和显著性检验
  3. P值

31丨统计意义（下）：如何通过显著性检验，判断你的A-B测试结果是不是巧合？

对于正态分布的数据，可以采用方差分析（Analysis of Variance, ANOVA），也叫F检验。有了F值，我们需要根据F检验值的临界表来查找对应的P值。

对于非正态分布的数据，我们也可以使用非参数的分析。常见的非参数检验包括二项分布检验、K-S 检验、卡方检验等等。

32丨概率统计篇答疑和总结为什么会有欠拟合和过拟合？

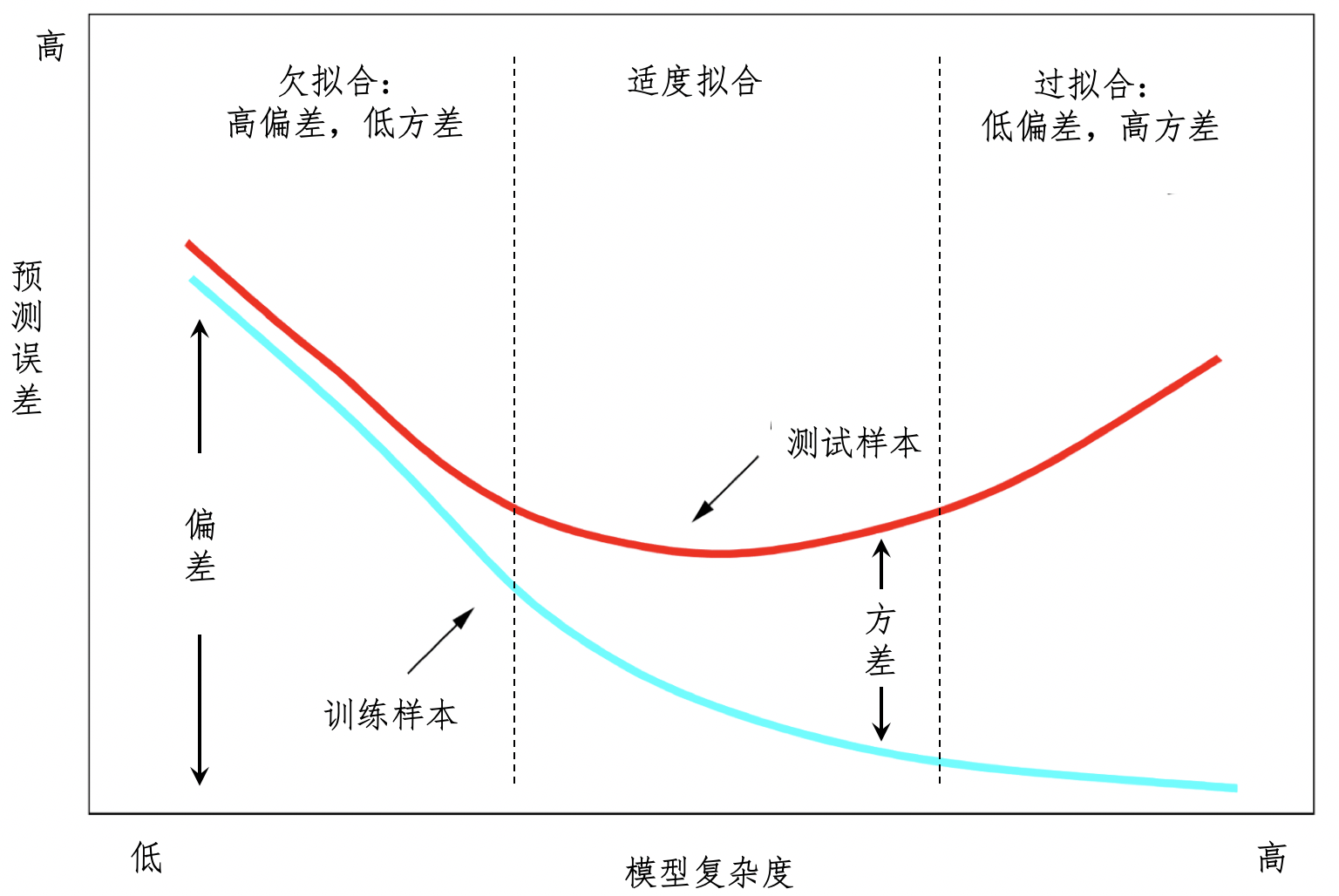
什么是欠拟合/过拟合

在监督式学习过程中，适度拟合、欠拟合和过拟合，这三种状态是逐步演变的。

20220531欠拟合过拟合.png

如何处理欠拟合和过拟合？

欠拟合

欠拟合问题，产生的主要原因是特征维度过少，拟合的模型不够复杂，无法满足训练样本，最终导致误差较大。因此，我们就可以增加特征维度，让输入的训练样本具有更强的表达能力。

之前讲解朴素贝叶斯的时候，我提到“任何两个变量是相互独立的假设”，这种假设和马尔科夫假设中的一元文法的作用一致，是为了降低数据稀疏程度、节省计算资源所采取的措施。可是，这种假设在现实中往往不成立，所以朴素贝叶斯模型的表达能力是非常有限的。当我们拥有足够的计算资源，而且希望建模效果更好的时候，我们就需要更加精细、更加复杂的模型，我们完全可以放弃朴素贝叶斯中关于变量独立性的假设，而使用二元、三元甚至更大的 N 元文法来处理这些数据。这就是典型的通过增加更多的特征，来提升模型的复杂度，让它从欠拟合阶段往适度拟合阶段靠拢。

过拟合

过拟合问题产生的主要原因则是特征维度过多，导致拟合的模型过于完美地符合训练样本，但是无法适应测试样本或者说新的数据。所以我们可以减少特征的维度。

之前在介绍决策树的时候，我提到了这类算法比较容易过拟合，可以使用剪枝和随机森林来缓解这个问题。

剪枝，顾名思义，就是删掉决策树中一些不是很重要的结点及对应的边，这其实就是在减少特征对模型的影响。虽然去掉一些结点和边之后，决策树对训练样本的区分能力变弱，但是可以更好地应对新数据的变化，具有更好的泛化能力。至于去掉哪些结点和边，我们可以使用前面介绍的特征选择方法来进行。

随机森林的构建过程更为复杂一些。“森林”表示有很多决策树，可是训练样本就一套，那这些树都是怎么来的呢？随机森林算法采用了统计里常用的可重复采样法，每次从全部 n 个样本中取出 m 个，然后构建一个决策树。重复这种采样并构建决策树的过程若干次，我们就能获得多个决策树。对于新的数据，每个决策树都会有自己的判断结果，我们取大多数决策树的意见作为最终结果。由于每次采样都是不完整的训练集合，而且有一定的随机性，所以每个决策树的过拟合程度都会降低。

从另一个角度来看，过拟合表示模型太复杂，而相对的训练数据量太少。因此我们也可以增加训练样本的数据量，并尽量保持训练数据和测试数据分布的一致性。如果我们手头上有大量的训练数据，则可以使用交叉验证（Cross Validation）的划分方式来保持训练数据和测试数据的一致性。其核心思想是在每一轮中，拿出大部分数据实例进行建模，然后用建立的模型对留下的小部分实例进行预测，最终对本次预测结果进行评估。这个过程反复进行若干轮，直到所有的标注样本都被预测了一次而且仅一次。如果模型所接受的数据总是在变化，那么我们就需要定期更新训练样本，重新拟合模型。

05-线性代数篇 (13讲)

33丨线性代数：线性代数到底都讲了些什么？

标量，向量，向量空间

向量运算

向量运算的几何意义

矩阵运算

乘法，转置，单位矩阵，逆矩阵

34丨向量空间模型：如何让计算机理解现实事物之间的关系？

向量空间模型

  1. 向量之间的距离
  2. 向量的长度
  3. 向量之间的夹角，夹角余弦

向量空间模型与机器学习

由于夹角余弦的取值范围已经在-1到1之间，而且越大表示越相似，所以可以直接作为相似度的取值。相对于夹角余弦，欧氏距离ED的取值范围可能很大，而且和相似度呈现反比关系，所以通常要进行1/(1-ED)这种归一化。

当ED为0的时候，变化后的值就是1，表示相似度为1，完全相同。当ED趋向于无穷大的时候，变化后的值就是0，表示相似度为0，完全不同。所以，这个变化后的值，取值范围是0到1之间，而且和相似度呈现正比关系。

早在上世纪的70年代，人们把向量空间模型运用于信息检索领域。由于向量空间可以很形象地表示数据点之间的相似程度，因此现在我们也常常把这个模型运用在基于相似度的一些机器学习算法中，例如K近邻（KNN）分类、K均值（K-Means)聚类等等。

35丨文本检索：如何让计算机处理自然语言？

36丨文本聚类：如何过滤冗余的新闻？

37丨矩阵（上）：如何使用矩阵操作进行PageRank计算？

我们可以把向量看作一维数组，把矩阵看作二维数组。矩阵的点乘，是由若干个向量的点乘组成的，所以我们可以通过矩阵的点乘操作，挖掘多组向量两两之间的关系。

我们讲了矩阵的点乘操作在PageRank算法中的应用。通过表示网页的邻接二元关系，我们可以使用矩阵来计算PageRank的得分。在这个应用场景下，矩阵点乘体现了多个马尔科夫过程中的状态转移。

矩阵点乘和其他运算操作，还可以运用在很多其他的领域。例如，我在上一节介绍K均值聚类算法时，就提到了需要计算某个数据点向量、其他数据点向量之间的距离或者相似度，以及使用多个数据点向量的平均值来获得质心点的向量，这些都可以通过矩阵操作来完成。

另外，在协同过滤的推荐中，我们可以使用矩阵点乘，来实现多个用户或者物品之间的相似程度，以及聚集后的相似程度所导致的最终推荐结果。下一节，我会使用矩阵来表示用户和物品的二元关系，并通过矩阵来计算协同过滤的结果。

38丨矩阵（下）：如何使用矩阵操作进行协同过滤推荐？

矩阵中的二维关系，除了可以表达图的邻接关系，还可以表达推荐系统中用户和物品的关系。这个关系是推荐系统的核心。

我们用矩阵 X 来表示用户对物品喜好程度：

20220531协同过滤推荐系统.png

其中第i行是第i个用户的数据，而第j列是用户对第j格物品的喜好程度。我们用xij表示这个数值。这里的喜好程度可以是用户购买商品的次数、对书籍的评分等等。

假设我们用一个0到1之间的小数表示。有了这种矩阵，我们就可以通过矩阵的操作，充分挖掘用户和物品之间的关系。下面，我会使用经典的协同过滤算法，来讲解矩阵在其中的运用。

基于用户的协同过滤

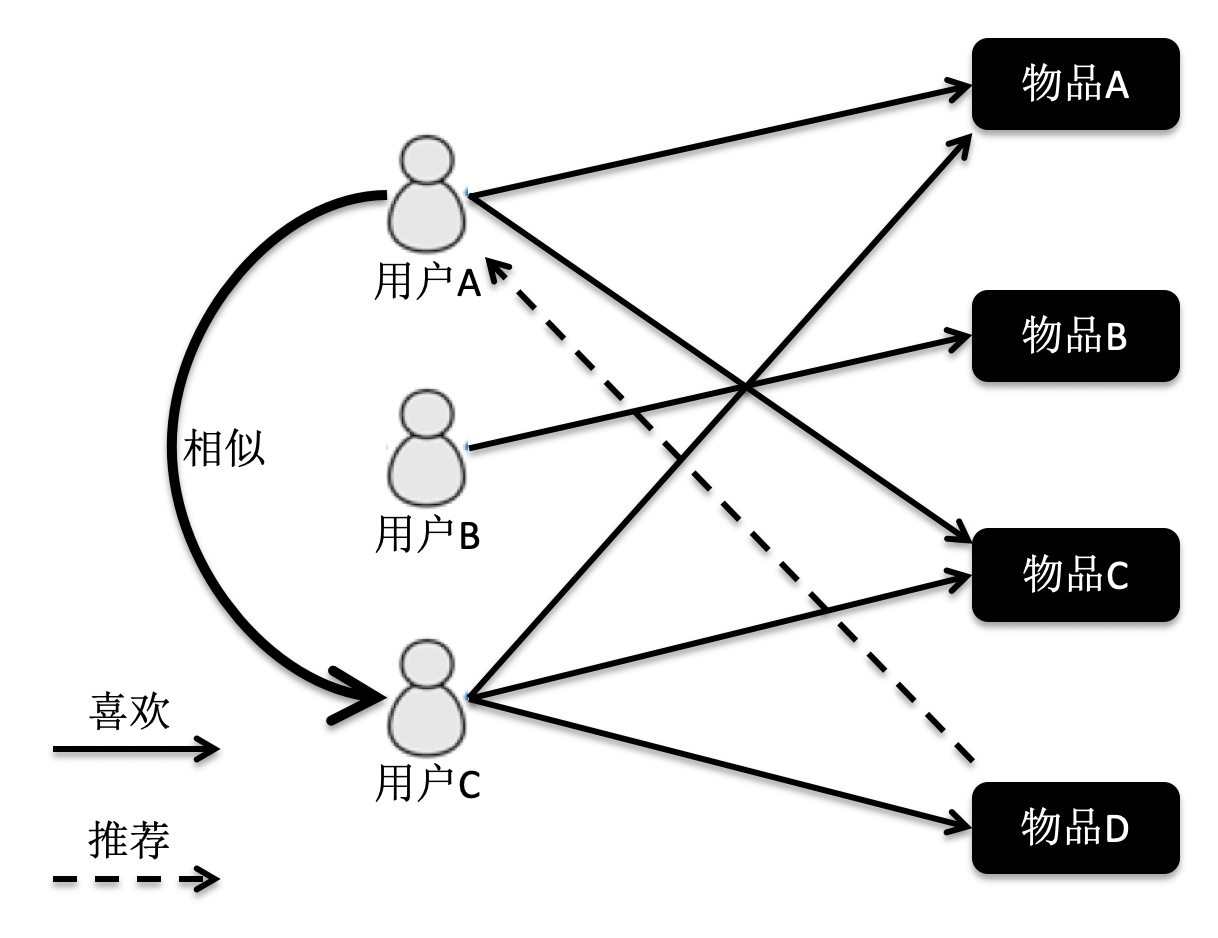
20220531协同过滤基于用户.png

根据这张图的访问关系来看，用户A访问了物品A和C，用户B访问了物品B，用户C访问了物品A，C和D。我们计算出来，用户C是A的近邻，而B不是。因此系统会更多地向用户A推荐用户C访问的物品D。

基于用户的协同过滤的核心公式如下：

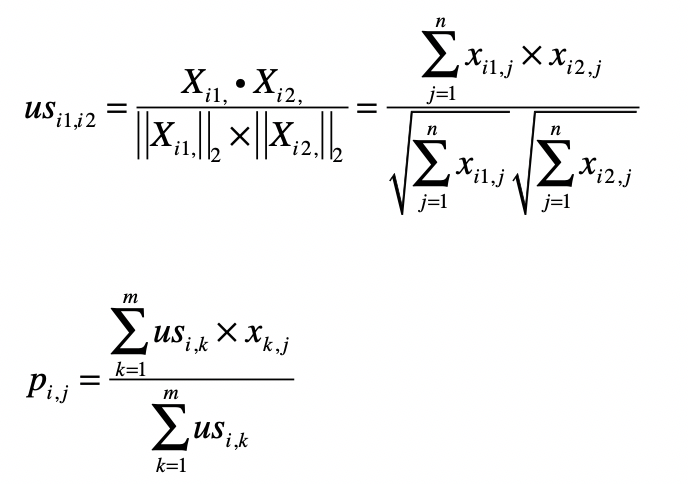
20220531基于用户协同过滤公式1.png

  1. 第一个公式是计算用户和用户之间的相似度。完成了这一步我们就能找到给定用户的“近邻”。
  2. 第二个公式利用第一个公式所计算的用户间相似度，以及用户对物品的喜好度，预测任一个用户对任一个物品的喜好度。其中pij表示第i用户对第j个物品的喜好度。

基于物品的过滤

基于物品的协同过滤是指利用物品相似度，而不是用户间的相似度来计算预测值。

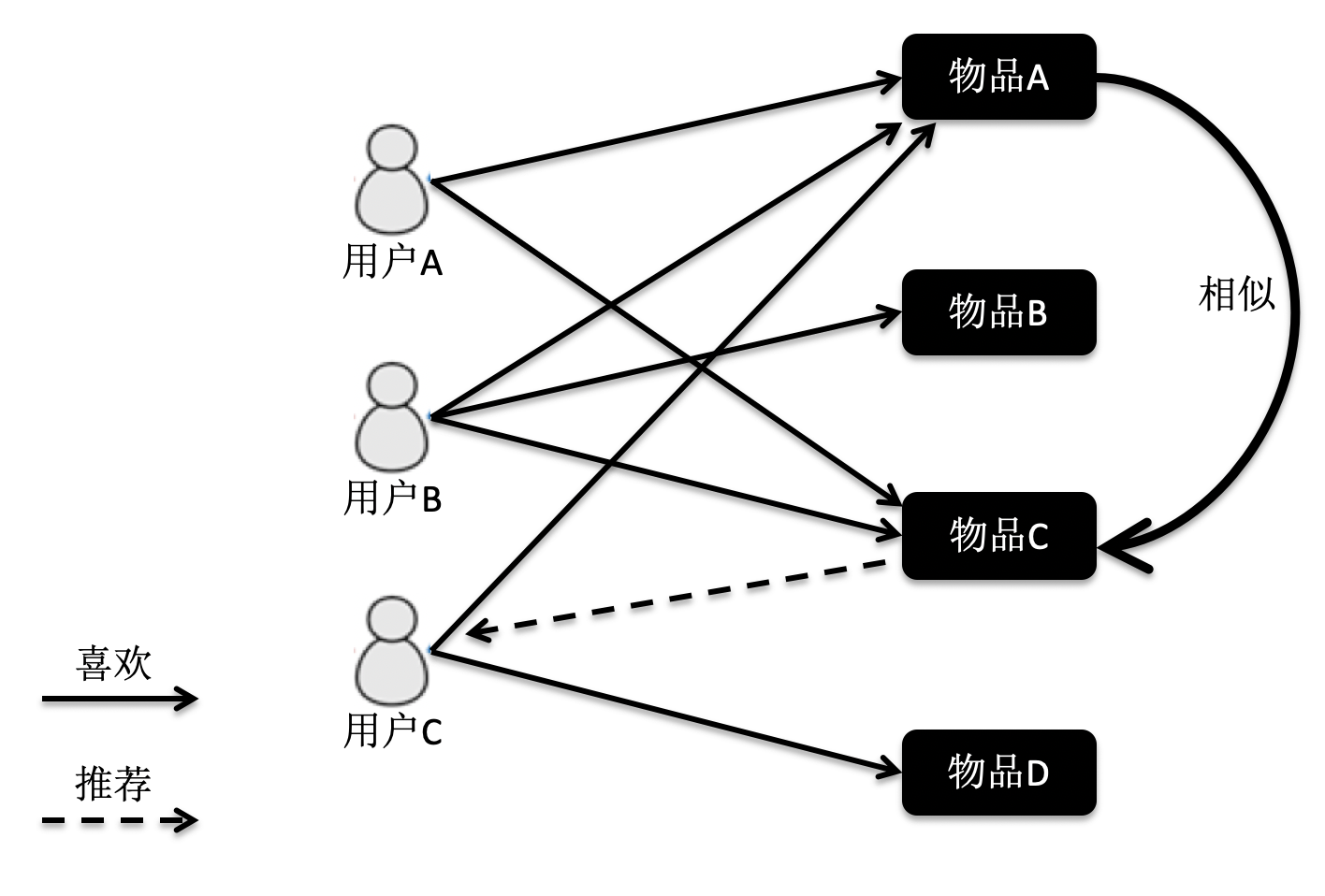
20220531基于物品的协同过滤图.png

在这张图中，物品A和C因为都被用户A和B同时访问，因此它们被认为相似度更高。当用户C访问过物品A后，系统会更多地向用户推荐物品C，而不是其他物品。

基于用户的协同过滤同样有两个公式:

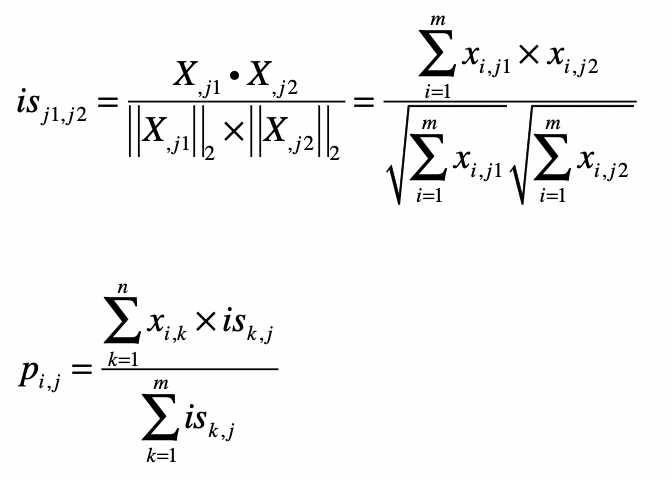
20220531基于物品的协同过滤公式.png

  1. 第一个公式的核心思想是计算物品和物品之间的相似度。
  2. 第二个公式利用第一个公式所计算的物品间相似度，和用户对物品的喜好度，预测任一个用户对任一个物品的喜好度。

协同过滤的公式（基于用户/物品）都可以用矩阵操作表达。

总结

今天我首先简要地介绍了推荐系统的概念和主要思想。为了给用户提供可靠的结果，推荐系统需要充分挖掘历史数据中，用户和物品之间的关系。协同过滤的推荐算法就很好地体现了这一点。

一旦涉及用户和物品的这种二元关系，矩阵就有用武之地了。我通过矩阵来表示用户和物品的关系，并通过矩阵计算来获得协同过滤的结果。协同过滤分为基于用户的过滤和基于物品的过滤两种，它们的核心思想都是相同的，因此矩阵操作也是类似的。在这两个应用场景下，矩阵点乘体现了多个用户或者物品之间的相似程度，以及聚集后的相似程度所导致的最终推荐结果。

当然，基于用户和物品间关系的推荐算法有很多，对矩阵的操作也远远不止点乘、按行求和、元素对应乘除法。我后面会介绍如何使用矩阵的主成分分析或奇异值分解，来进行物品的推荐。

39丨线性回归（上）：如何使用高斯消元求解线性方程组？

高斯消元

矩阵操作实现高斯消元求解线性方程组。

高斯消元法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说，消元就是把系数矩阵变为上三角矩阵，而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵，用于由系数和因变量值组成的增广矩阵，并获得最终的方程解。

线性方程组与线性回归分析

线性方程组的概念，也是线性回归分析的基础。它们有两个最主要的区别。

  1. 第一个区别是，在线性回归分析中，样本数据会告诉我们自变量和因变量的值，要求的是系数。而在线性方程组中，我们已知系数和因变量的值，要求的是自变量的值。
  2. 第二个区别是，在线性回归分析中，方程的数量要远远大于自变量的数量，而且我们不要求每个方程式都是完全成立。这里，不要求完全成立的意思是，拟合出来的因变量值可以和样本数据给定的因变量值存在差异，也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了，所以你应该能理解，模型的拟合不可能 100% 完美，这和我们求解线性方程组精确解的概念是不同的。

正是因为这两点差异，我们无法直接使用消元法来求解线性回归，而是使用最小二乘法来解决线性回归的问题。

40丨线性回归（中）：如何使用最小二乘法进行直线拟合？

41丨线性回归（下）：如何使用最小二乘法进行效果验证？

从广义上来说，最小二乘法不仅可以用于线性回归，还可以用于非线性的回归。其主要思想还是要确保误差ε最小，但是由于现在的函数是非线性的，所以不能使用求多元方程求解的办法来得到参数估计值，而需要采用迭代的优化算法来求解，比如梯度下降法、随机梯度下降法和牛顿法。

42丨PCA主成分分析（上）：如何利用协方差矩阵来降维？

在概率统计模块，我详细讲解了如何使用各种统计指标来进行特征的选择，降低用于监督式学习的特征之维度。接下来的几节，我会阐述两种针对数值型特征，更为通用的降维方法，它们是主成分分析 PCA（Principal Component Analysis）和奇异值分解 SVD（Singular Value Decomposition）。这两种方法是从矩阵分析的角度出发，找出数据分布之间的关系，从而达到降低维度的目的。

PCA 分析法的主要步骤

对于m×n维的样本矩阵，其中每一行表示一个样本，而每一列表示一维特征。现在，我们的问题是，能不能通过某种方法，找到一种变换，可以降低这个矩阵的列数，也就是特征的维数，并且尽可能的保留原始数据中有用的信息？

针对这个问题，PCA 分析法提出了一种可行的解决方案。它包括了下面这样几个主要的步骤：

  1. 标准化样本矩阵中的原始数据；
  2. 获取标准化数据的协方差矩阵；
  3. 计算协方差矩阵的特征值和特征向量；
  4. 依照特征值的大小，挑选主要的特征向量；
  5. 生成新的特征。

标准化原始数据

之前我们已经介绍过特征标准化，这里我们需要进行同样的处理，才能让每维特征的重要性具有可比性。需要注意的是，这里标准化的数据是针对同一种特征，也是在同一个特征维度之内。不同维度的特征不能放在一起进行标准化。

获取协方差矩阵

首先，来看一下什么是协方差（Covariance），以及协方差矩阵。

协方差是用于衡量两个变量的总体误差。假设两个变量分别是 x 和 y，而它们的采样数量都是 m，那么协方差的计算公式就是如下这种形式：

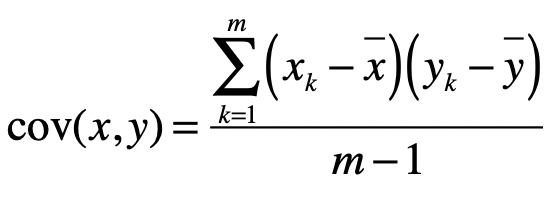
20220531协方差公式.png

而当两个变量是相同时，协方差就变成了方差。

对于m×n维的样本矩阵，其协方差矩阵（i,j)位置处的值表示第i个特征（列向量）和第j个特征（列向量）之间的协方差，公式如下：

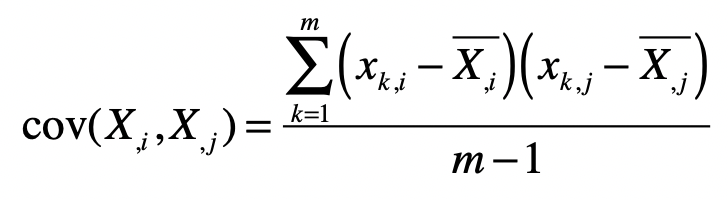
20220531协方差矩阵ij位置元素.png

所以，样本矩阵的协方差矩阵就可以表示为：

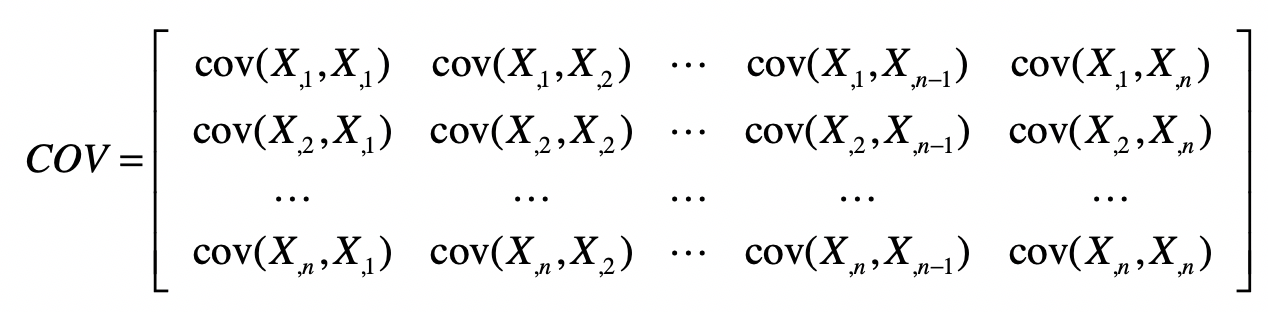
20220531协方差矩阵公式.png

从协方差的定义可以看出，协方差矩阵是个对称矩阵。另外，这个对称矩阵的主对角线上的值就是各维特征的方差。

计算协方差矩阵的特征值和特征向量

需要注意的是，这里所说的矩阵的特征向量，和机器学习中的特征向量（Feature Vector）完全是两回事。矩阵的特征值和特征向量是线性代数中两个非常重要的概念。对于一个矩阵X，如果能找到向量v和标量λ，使得下面这个式子成立。

Xv=λv

那么，我们就说v是矩阵X的特征向量，而λ是矩阵X的特征值。矩阵的特征向量和特征值可能不止一个。说到这里，你可能会好奇，特征向量和特征值表示什么意思呢？我们为什么要关心这两个概念呢？简单的来说，我们可以把向量v左乘一个矩阵X看做对v进行旋转或拉伸，而这种旋转和拉伸都是由于左乘矩阵X后，所产生的“运动”所导致的。特征向量v表示了矩阵X运动的方向，特征值λ表示了运动的幅度，这两者结合就能描述左乘矩阵X所带来的效果，因此被看作矩阵的“特征”。在PCA中的主成分，就是指特征向量，而对应的特征值的大小，就表示这个特征向量或者说主成分的重要程度。特征值越大，重要程度越高，我们要优先现在这个主成分，并利用这个主成分对原始数据进行变换。

挑选主要的特征向量，转换原始数据

假设我们获得了k个特征值和对应的特征向量，按照所对应的λ数值的大小，对这k组的特征向量进行排序。排名靠前的特征向量就是最重要的特征向量。

假设我们只取前k1个最重要的特征，那么我们使用这k1个特征向量，组成一个n×k1维的矩阵D。

把包含原始数据的m×n维矩阵X左乘矩阵D，就能重新获得一个m×k1维的矩阵，达到了降维的目的。

有的时候，我们无法确定k1取多少合适。一种常见的做法是，看前k1个特征值的和占所有特征值总和的百分比。假设一共有10个特征值，总和是100，最大的特征值是80，那么第一大特征值占整个特征值之和的80%，我们认为它能表示80%的信息量，还不够多。那我们就继续看第二大的特征值，它是15，前两个特征值之和有95，占比达到了95%，如果我们认为足够了，那么就可以只选前两大特征值，把原始数据的特征维度从10维降到2维。

43丨PCA主成分分析（下）：为什么要计算协方差矩阵的特征值和特征向量？

这一部分分析的太到位了，将原文链接放上：PCA主成分分析（下）：为什么要计算协方差矩阵的特征值和特征向量？。

基于Python的案例分析

通过基于Python的案例来一步步计算PCA的各个步骤的中间结果。

PCA背后的核心思想

为什么要使用协方差矩阵？

为什么我们要使用样本数据中，各个维度之间的协方差，来构建一个新的协方差矩阵？要弄清楚这一点，首先要回到PCA最终的目标：降维。降维就是要去除那些表达信息量少，或者冗余的维度。

  1. 我们首先来看如何定义维度的信息量大小。这里我们认为样本在某个特征上的差异越大，这个特征包含的信息量就越大，就越重要。很自然，我们就能想到使用某维特征的方差来定义样本在这个特征维度上的差异。
  2. 另一方面，我们要看如何发现冗余的信息。如果两种特征是有很高的相关性，那我们可以从一个维度的值推算出另一个维度的值，所表达的信息就是重复的。在实际运用中，我们可以使用皮尔森（Pearson）相关系数，来描述两个变量之间的线性相关程度。这个系数的取值范围是[−1,1]，绝对值越大，说明相关性越高，正数表示正相关，负数表示负相关。在本质上，皮尔森相关系数和数据标准化后的协方差是一致的。

考虑到协方差既可以衡量信息量的大小，也可以衡量不同维度之间的相关性，因此我们就使用各个维度之间的协方差所构成的矩阵，作为PCA分析的对象。就如前面说讲述的，这个协方差矩阵主对角线上的元素是各维度上的方差，也就体现了信息量，而其他元素是两两维度间的协方差，也就体现了相关性。

既然协方差矩阵提供了我们所需要的方差和相关性，那么下一步，我们就要考虑对这个矩阵进行怎样的操作了。

为什么要计算协方差矩阵的特征值和特征向量？

关于这点，我们可以从两个角度来理解。

第一个角度是对角矩阵。所谓对角矩阵，就是说只有矩阵主对角线之上的元素有非0值，而其他元素的值都为0。我们刚刚解释了协方差矩阵的主对角线上，都是表示信息量的方差，而其他元素都是表示相关性的协方差。既然我们希望尽可能保留大信息量的维度，而去除相关的维度，那么就意味着我们希望对协方差进行对角化，尽可能地使得矩阵只有主对角线上有非0元素。

假如我们确实可以把矩阵尽可能的对角化，那么对角化之后的矩阵，它的主对角线上元素就是、或者接近矩阵的特征值，而特征值本身又表示了转换后的方差，也就是信息量。而此时，对应的各个特征向量之间是基本正交的，也就是相关性极低甚至没有相关性。

第二个角度是特征值和特征向量的几何意义。在向量空间中，对某个向量左乘一个矩阵，实际上是对这个向量进行了一次变换。在这个变换的过程中，被左乘的向量主要发生旋转和伸缩这两种变化。如果左乘矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，而伸缩的比例就是特征值。换句话来说，某个矩阵的特征向量表示了这个矩阵在空间中的变换方向，这些方向都是趋于正交的，而特征值表示每个方向上伸缩的比例。

如果一个特征值很大，那么说明在对应的特征向量所表示的方向上，伸缩幅度很大。这也是为什么，我们需要使用原始的数据去左乘这个特征向量，来获取降维后的新数据。因为这样做可以帮助我们找到一个方向，让它最大程度地包含原有的信息。需要注意的是，这个新的方向，往往不代表原始的特征，而是多个原始特征的组合和缩放。

44丨奇异值分解：如何挖掘潜在的语义关系？

今天，我们来聊另一种降维的方法，SVD奇异值分解（SingularValueDecomposition）。它的核心思路和PCA不同。PCA是通过分析不同纬特征之间的协方差，找到包含最多信息量的特征向量，从而实现降维。而SVD这种方法试图通过样本矩阵本身的分解，找到一些“潜在的因素”，然后通过把原始的特征维度映射到较少的潜在因素之上，达到降维的目的。

方阵的特征分解

  • 方阵
  • 酉矩阵
  • 方阵的特征分解

那么如果X不是方阵，那么应该如何进行矩阵的分解呢？这个时候就需要用到奇异值分解SVD了。

SVD分解

潜在语义分析和SVD

45丨线性代数篇答疑和总结：矩阵乘法的几何意义是什么？

06-综合应用篇 (6讲)

46丨缓存系统：如何通过哈希表和队列实现高效访问？

缓存设计的几个主要考量因素: 1. 硬件性能：高性能做低性能的缓存。 2. 命中率。缓存删除策略： 1. 最少使用 LFU（Least Frequently Used）策略 2. 最久未用 LRU（Least Recently Used）策略：使用队列（Queue）表示上次使用时间，刚用过的放在队尾，淘汰的时候直接淘汰队头的即可。 3. 更新周期

我们同时使用了哈希函数和队列，实现了一个最简单的缓存系统。哈希函数确保了查找的高效率，而队列则实现了LRU的淘汰策略。通过这两点，你就能理解缓存设计的基本原理和方法。

47丨搜索引擎（上）：如何通过倒排索引和向量空间模型，打造一个简单的搜索引擎？

搜索引擎最重要的核心就是及时性和相关性。及时性确保用户可以快速找到信息，而相关性确保所找到的信息是用户真正需要的。 1. 倒排索引是搜索引擎提升及时性中非常关键的一步。倒排索引非常适合使用哈希表，特别是链地址型的哈希表来实现。 2. 向量空间模型可以作为文本搜索的相关性模型。但是，它的计算需要把查询和所有的文档进行比较，时间复杂度太高，影响了及时性。这个时候，我们可以利用倒排索引，过滤掉绝大部分不包含查询关键词的文档。

48丨搜索引擎（下）：如何通过查询的分类，让电商平台的搜索结果更相关？

相关性模型是搜索引擎非常核心的模块，它直接影响了搜索结果是不是满足用户的需求。我们之前讲解的向量空间模型、概率语言模型等常见的模型，逐渐成为了主流的相关性模型。不过这些模型通常适用于普通的文本检索，并没有针对每个应用领域进行优化。

在电商平台上，搜索引擎是帮助用户查找商品的好帮手。可是，直接采用向量空间模型进行排序往往效果不好。这主要是因为索引的标题和属性都很短，我们无法充分利用关键词的词频、逆文档频率等信息。考虑到搜索商品的时候，商品的分类对于用户更为重要，所以我们在设计相关性排序的时候需要考虑这个信息。

为了识别用户对哪类商品更感兴趣，我们可以对用户输入的查询进行分类。用于构建分类器的数据，可以是运营人员发布的商品目录信息，也可以是用户使用之后的行为日志。我们可以根据搜索系统运行的情况，赋予它们不同的权重。

如果我们可以对查询做出更为准确的分类，那么就可以使用这个分类的结果，来对原有搜索结果进行重新排序。现在的开源搜索引擎，例如Elasticsearch，都支持动态修改排序结果，为我们结合分类器和搜索引擎提供了很大的便利。

49丨推荐系统（上）：如何实现基于相似度的协同过滤？

原文链接：49丨推荐系统（上）：如何实现基于相似度的协同过滤？.html

通过一个常用的实验数据，设计并实现了最简单的基于用户的协同过滤。值得动手练习一下。

50丨推荐系统（下）：如何通过SVD分析用户和物品的矩阵？

原文链接：50丨推荐系统（下）：如何通过SVD分析用户和物品的矩阵？.html

通过Python示例，解释了SVD分解过程中的数学量的物理意义，值得上手一试。

在用户对电影评分的应用场景下，SVD分解后的U矩阵、V矩阵和Σ矩阵各自代表的意义，其中Σ矩阵中的奇异值表示了SVD挖掘出来的电影主题，U矩阵中的奇异向量表示用户对这些电影主题的评分，而V矩阵中的奇异向量表示了电影和这些主题的相关程度。

分解之后所得到的奇异值σ对应了一个“主题”，σ值的大小表示这个主题在整个电影集合中的重要程度，而V中的右奇异向量表示每部电影和这些“主题”的关系强弱。

51丨综合应用篇答疑和总结：如何进行个性化用户画像的设计？

07-加餐 (3讲)

数学专栏课外加餐（一）丨我们为什么需要反码和补码？

数学专栏课外加餐（三）：程序员需要读哪些数学书？

数学专栏课外加餐（二）丨位操作的三个应用实例

08-结束语 (1讲)

结束语丨从数学到编程，本身就是一个很长的链条